Распространение пучков с большим нормированным первеансом, страница 4

При плотностях заряженных частиц, характерных для ионных пучков, плазму можно считать бесстолкновительной и, следуя изложенной в разд. 3.5 теории Ленгмюра — Тонкса, предположить, что ионы возникают в пучке с нулевой скоростью. Это предположение пригодно и тогда, когда ионы проявляются в результате переноса заряда, поскольку сечения переноса заряда велики по сравнению с сечениями упругого рассеяния. Как и в случае плазмы, не содержащей быстрой ионной компоненты, пространство между ограничивающими электродами будет состоять из области, в которой отклонение от зарядовой нейтральности очень мало и применимо плазменное приближение n_e≃n_i, и слоев, в которых превалирует пространственный заряд ионов.

Ограничимся для простоты анализом длинного ленточного пучка с однородной плотностью быстрых ионов n_b. Поперечное сечение пучка имеет высоту b и ширину 2а, причем b≫2а; длина l пучка, т. е. расстояние между источником и мишенью, также удовлетворяет условию l≫2а. Предположим, что медленные ионы генерируются в плазме со скоростью g. Их скорость задается выражением (3.30)

,                                             (3.30)

где υ— скорость ионов, возникающих в точке х₁, на расстоянии х от медианной плоскости. Тогда

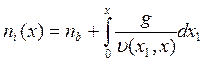                                                  ,                                                      (6.1)

т. е. (3.29) прибавляется плотность ионов пучка n_b.

В области плазмы полагаем n_i=n_e и

.

Потенциал V выбран равным нулю в медианной плоскости, где n_e=n₀, Т— электронная температура. Уравнение плазмы имеет вид

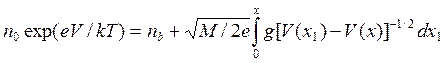                            .                                 (6.2)

Как и ранее, вводим

                                                                                                            (3.34)

и

                                                  ,                                                      (3.34)

где длина L задается выражением (3.39); из (3.37) при γ=0 она равна

                                             .                                                  (6.3)

Тогда уравнение плазмы (6.2) запишем в виде

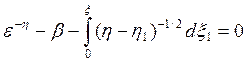                                             ,                                                  (6.4)

где

                                                             .(6.5)

За исключением константы β, уравнение (6.4) идентично уравнению (3.41) при γ=0. Рассмотрение, полностью аналогичное проведенному Харрисоном и Томпсоном [124], которые получили решение (3.41), приводит к решению

                                                  ,                                                      (6.6)

где

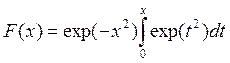                                                                                                             (2.129)

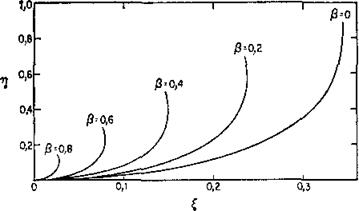
есть введенный ранее интеграл Доусона. При β=0 уравнение (6.6) переводит, как и следует, в (3.42), поскольку малое β соответствует ситуации, когда ионы пучка составляют лишь малую долю от полной плотности ионов. В этом случае пучковая плазма переходит в обычную плазму. Величина β, близкая к единице, соответствует случаю, когда почти все ионы являются ионами пучка. На рис. 6.3 показана зависимость η(ξ) (6.6) при разных значениях β.

Каждая из этих кривых ведет себя так же, как и кривая при β=0, т. е. в случае обычной плазмы, рассмотренном в разд. 3.5, но значения η₀ и ξ₀ зависят от β. Поскольку

                                                         ,                                                             (6.7)

производную от правой части (6.6) можно приравнять нулю при η≃η₀. Это дает

, или

                                                      .                                                           (6.8)

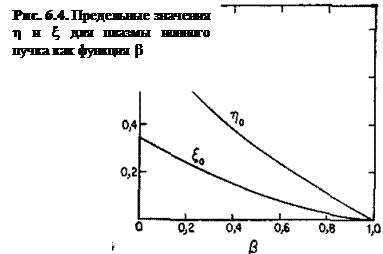
График зависимости η₀(β) в диапазоне 0<β<1 приведен на рис. 6.4. Соответствующие значения ξ₀ получатся при подстановке (6.8) в (6.6):

                                                                                         (6.9)

и также показаны на рис. 6.4 в графической форме. Как и в случае плазмы без пучка, точные решения должны отличаться от (6.6) или от кривых рис. 6.3 при ξ→ξ₀ и иметь переход к решению в слое, как показано схематически на pиc. 3.6.