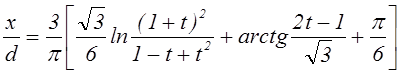,
(7.4.10)
где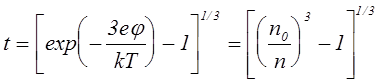 
, а
плотность ионного тока определяется следующим соотношением
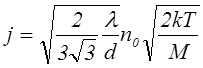(7.4.11)
Переходя к рассмотрению общего случая введем безразмерную переменную
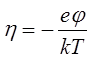(7.4.12)
и параметры
, а
= j / j0 (7.4.13)
и преобразуем (7.4.2) к следующему виду
j0 exp(-h) = exp(-x/l)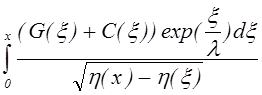 
(7.4.2¢¢)
Умножая на dh/dx и интегрируя по dx от 0 до y получаем после преобразований интегральное уравнение для потенциала.
h(y) = - ln(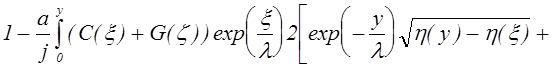
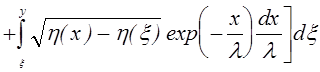. (7.4.14)
Теперь получим уравнение
для для определения коэффициента a. Умножая (7.4.2¢¢) на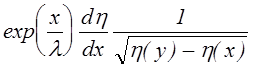 
и
интегрируя по dx от 0 до y получаем
= 
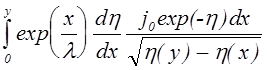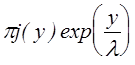. (7.4.15)
При x=d производная dh/dx ®¥, и, соответственно, dj/dh=0. Тогда после некоторых преобразований получаем,
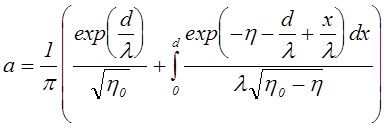(7.4.16)
Система уравнений (7.4.14), (7.4.16) решалась методом последовательных приближений. В ходе вычислений были рассчитаны распределение потенциала в промежутке и найдены значения коэффициента а для значений параметра l/d от 0.05 до бесконечности. Как следует из результатов расчетов при уменьшении параметра l/d возрастает перепад потенциала на плазме (см. рис.7.15), а ток ионной эмиссии уменьшается (см. рис.7.16). При больших и малых l/d результаты расчетов совпадают с рассмотренными выше предельными случаями.
Отметим, что результаты расчетов плотности тока ионной эмиссии во всем исследованном диапазоне значений параметра l/d от 0.05 до бесконечности можно с хорошей точностью описать простыми аппроксимационными соотношениями. В первом случае (G(x)~const) для оценки плотности тока ионной эмиссии можно использовать соотношение
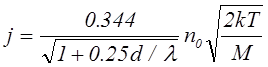(7.4.17)
а во втором (G(x)~n(x))
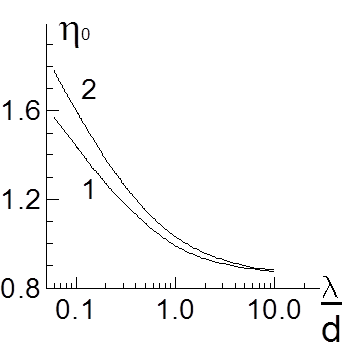
Рис. 7.15. Зависимости перепада потенциала на плазме от параметра l/d. 1 - G ~ const, 2 - G = nine(x).
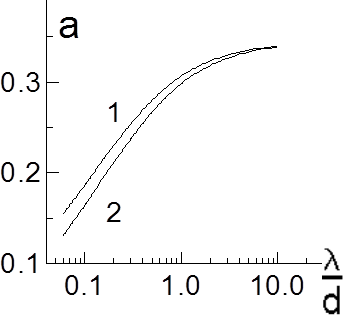
Рис. 7.16. Зависимости коэффицента а от параметра l/d.
1 - G ~ const, 2 - G = nine(x).
.
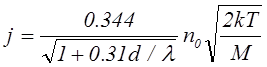(7.4.18)
В целом можно сказать, что вплоть до значений l/d ~ 1 можно с достаточной точностью использовать выражение, полученное в бесстолкновительном случае, и лишь при меньших l/d величина тока ионной эмиссии начинает быстро уменьшаться.
Выводы
В результате проведенных исследований анализа влияния ионной эмисии на характеристики разряда с полым катодом показано что сушествует некоторый, зависящий от давления, оптимальный уровень эффективности извлечения, при котором энергетическая эффективность достигает максимального значения. При дальнейшем увеличении эффективности извлечения энергетическая эффективность начинает уменьшаться вследствие затруднеия условий поддержания разряда и резким ростом напряжения горения. Величина оптимального уровня ионной эмиссии возрастает с увеличением давления и достигает 0.5 при давлениях, существенно превышающих критическое.
Проведен сравнительный анализ ионной эмиссии для случаев, когда эмиттерный электрод находится под потенциалом катода тлеющего и дугового разрядов, и показано, что для получения пучков с большей плотностью тока необходимо уменьшение разности потенциалов между эмиттерным электродом и плазмой, что обеспечивается в дуговых разрядах или при плавающем потенциале эмиттерного электрода. В системах, где эмиттерный электрод находится под потенциалом катода тлеющего разряда, для получения заданной плотности тока необходимо усиление ускоряющего электрического поля.
Проведенные расчеты тока ионной эмиссии из плазмы при учете процесса резонансной перезарядки в диапазоне давлений, когда режим движения ионов меняется от бесстолкновительного до случая подвижности в сильных электрических полях, показывают, что с увеличением давления возрастает перепад потенциала на плазме, а плотность тока ионной эмиссии уменьшается. Предложеы простые аппроксимационные формулы для плотности ионного тока, которые с удовлетворительной точностью описывают полученные результаты, и из которых известное соотношение, полученное Ленгмюром для бесстолкновительного режима, вытекает как частный случай.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.