Ионная эмиссия из тлеющих разрядов с осциллирующими электронами, страница 2

Переходя к тем же безразмерным переменным, которые использовались в главе 2, получим из (7.1.3) следующее соотношение, связывающее обезразмеренные напряжение и давление

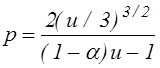.                                                                (7.1.4)

Полученное выражение имеет физический смысл, если знаменатель больше 0, т.е. при выполнении условия

u > 1/(1-a).                                                                        (7.1.5)

Иными словами при наличии эмиссии напряжение горения по крайней мере в 1/(1-a) раз превышает величину U₀. В указанной области функция р(u) также как и в режиме без ионной эмиссии является немонотонной и имеет в точке u=3/(1-a) минимум, равный . Cледовательно обратная к р(u) зависимость u(р) имеет область определения

p                                                                    (7.1.6)

и является в этой области двузначной. Вне этой области выполнение условия самостоятельности и стационарное горение разряда невозможно ни при каком значении u. В частности в отсутствии эмиссии из (7.1.6.) получаем, что горение разряда возможно при р>1, как этого и следовало ожидать. С увеличением эмиссии и при прочих равных условиях нижняя граница рабочего диапазона давлений постепенно возрастает, что требует увеличения напуска газа для поддержания разряда. Это накладывает определенные ограничения на возможность увеличения эффективности извлечения, так как с повышением напуска в разряд и соответствующим возрастанием давления в ускоряющем промежутке может произойти нарушение его электропрочности.

Зависимости u(p) для различных значений параметра a приведены на рис.7.1. Устойчивыми и реализуемыми в эксперименте являются нижние ветви приведенных зависимостей, что анализировалось в главе 2. Как видно из рисунка с увеличением эффективности уровень напряжения на этой ветви существенно возрастает. Это обстоятельство может сделать нецелесообразным чрезмерное увеличение эффективности извлечения, даже если электрическая прочность не будет нарушена, так как рост напряжения горения может привести к уменьшению энергетической эффективности источника

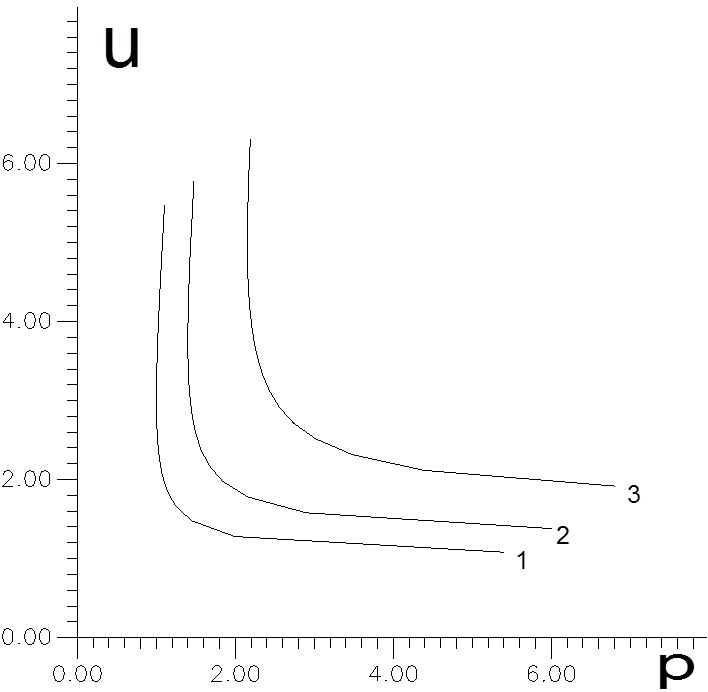
Рис.7.1. Зависимости u(p) для различных значений параметра a ,

 1 - 0, 2 - 0.2, 3 - 0.4.

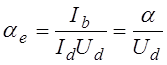                                                                  (7.1.7)

в том случае, если напряжение с увеличением a начнет расти быстрее, чем по линейному закону, т.е. если будет выполнятся условие dU/da > U /a.

Проанализируем эту ситуацию с целью определения оптимального значения a, при котором обеспечивается максимальная энергетическая эффективность источника. Введем безразмерную переменную

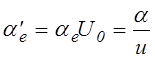.                                                                   (7.1.8)

Соотношение (7.7.4.) можно с помощью подстановки

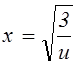                                                                                 (7.1.9)

преобразовать в кубичное уравнение, разрешив которое можно найти явное выражение для обезразмеренного разрядного напряжения. Для нижней устойчивой ветви оно выглядит следующим образом:

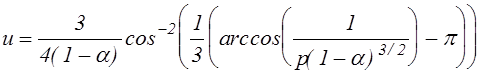.          (7.1.10)

Подставляя полученное выражение в (7.1.8) и рассматривая р как заданный параметр получим зависимость  в следующем виде

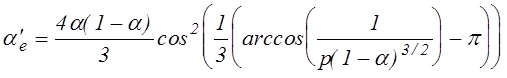      (7.1.11)

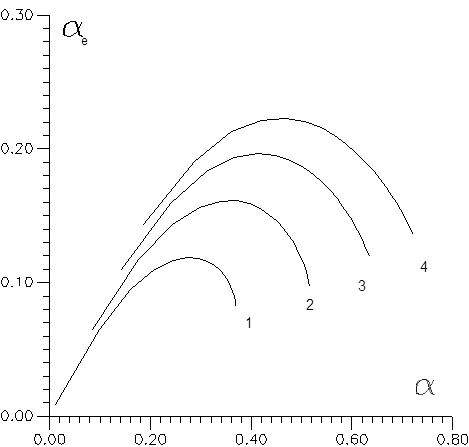
Рис.7.2. Зависимости  для разных давлений.

р: 1 - 2; 2 - 3; 3 - 5; 4 - 10.

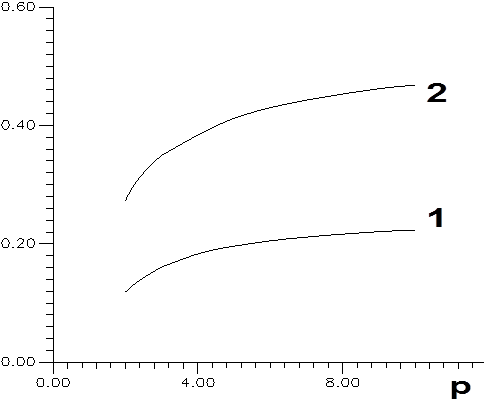
Рис.7.3. Функции: 1 -  ; 2 -

На рис.7.2 приведены рассчитанные по данному соотношению зависимости  для нескольких значений давления. Как видно из рисунка, все кривые имеют один и тот же качественный характер: начальный рост постепенно замедляется, кривые достигают в некоторой точке  максимума   а затем энергетическая эффективность уменьшается. Как  так и  возрастают с увеличением давления. Анализируя вид функции (7.1.11) нетрудно рассчитать эти зависимости. Функции  и   приведены на рис.7.3. Как видно из рисунка с увеличением р начальный рост сменяется насыщением и максимального значения энергетической эффективности  можно добится при давлениях, существенно больших 1, при эффективности извлечения 0.5. Таким образом для увеличения энергетической эффективности необходимо повышать напуск газа в источник, по крайней мере до тех пор, пока сохраняется электрическая прочность промежутка, либо пока напуск газа Q не превысит некоторого предельного значения, определяемого особенностями того или иного технологического процесса, для осуществления которого используется ионный пучок. Однако повышение напуска газа приведет к ухудшению другой важной характеристики источника - газовой экономичности