Движение ионов в ускоряющем промежутке источника, как правило, происходит в бесстолкновительном режиме, так как здесь давление газа должно быть низким для обеспечения высокой электрической прочности. В то же время в газоразрядной системе источника могут быть реализованы такие газовые условия, при которых длина пробега становится сравнимой с ее размерами. Это связано с наличием перепада давления между ускоряющей и газоразрядной системами источника, а также с тем, что размеры газоразрядной камеры могут быть существенно больше длины ускоряющего промежутка. В этих условиях использование для оценки ионного тока, поступающего из разрядной системы в ускоряющий промежуток, соотношений, полученных в бесстолкновительном случае, становится необоснованным. Необходимо их уточнение с учетом возможности процесса перезарядки. В настоящем разделе рассматривается влияние столкновений на величину тока ионной эмиссии в диапазоне давлений, при которых характер движения ионов меняется от бесстолкновительного режима, когда скорость иона определяется пройденной разностью потенциалов, до режима подвижности в сильных электрических полях, когда скорость иона пропорциональна квадратному корню из напряженности электрического поля.
Рассмотрим задачу в плоской геометрии, считая, что газоразрядная плазма находится между двумя плоскопараллельными пластинами, находящимися на расстоянии 2d друг от друга. Будем считать, что электроны распределены по закону Больцмана
ne(x) = n0
exp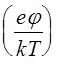
(7.4.1)
где ne - концентрация электронов, n0 - концентрация в центре системы. Для ионной концентрации при выполнении условия, что энергия, набираемая ионом на длине свободного пробега, существенно превышает тепловую энергию атомов газа, справедливо соотношение [87]
ni (x) =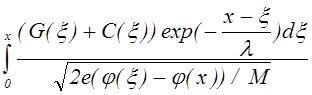 
(7.4.2)
где l - длина пробега до перезарядки, G - число ионов, генерируемых в единицу времени в единице объема в результате ионизации, C - число ионов, возникающих в единицу времени в единице объема в результате перезарядки. При этом
C(x) = j(x) / l =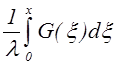 
(7.4.3)
где j(x) - плотность ионного тока в точке х. Концентрации ионов и электронов равны между собой
ne = ni = n, (7.4.4)
а нарушение квазинейтральности
происходит на пренебрежимо малом расстоянии от электродов, т.е при 
. В этой точке производные потенциала и
концентрации обращаются в бесконечность.
Будут рассмотрены две ситуации: в первом случае будем считать, что ионизация идет равномерно (G ~ const), а во втором случае ионизация осуществляется плазменными электронами G = nine(x), где ni- частота ионизации.
В бесстолкновительном режиме (l >> d) система уравнений упрощается и для связи плотности ионного тока, выходящего из плазмы, с ее параметрами в этом случае выполняется следующее соотношение [82],
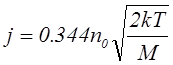(7.4.5)
которое справедливо для обоих рассматриваемых случаев.
При большом числе столкновений (l << d) записанную систему уравнений также можно упростить и получить аналитическое решение задачи. Пренебрежем в (2) величиной G по сравнению с С. Учитывая, что экспонента быстро стремится к 0 при удалении точки x от x заменим С(x) на С(х) и вынесем за знак интегрирования. В знаменателе разложим j(x) в ряд
j(x)=j(х)+ j¢(х)(x-х) (7.4.6)
и учитывая, что при больших х
,
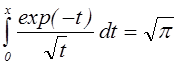(7.4.7)
получим
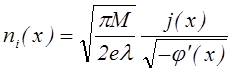(7.4.2¢)
Как видно из полученного выражения проведенная процедура упрощения эквивалентна принятию допущения, что ионы движутся в режиме подвижности в сильных полях.
Решение системы уравнений (7.4.1), (7.4.2¢), (7.4.4) в случае G = const дает следующее выражение для потенциала
j =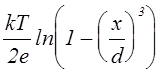 
(7.4.8)
а связь плотности тока ионной эмиссии из плазмы с ее параметрами имеет следующий вид
.
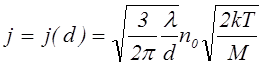(7.4.9)
В случае G(x) ~ n(x) координата и потенциал связаны следующим соотношением
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.