Таунсендовский разряд. Предельный ток Таунседовского разряда. Высоковольтный тлеющий разряд, страница 4

Тогда m=1 - еще одна форма записи условия самостоятельности. Пусть в момент времени t=0 на промежуток подали напряжение U, превышающее U_br и вследствие каких-то причин имеется начальный ток электронов из катода i₀. Начинается лавинообразное размножение электронов, которое заканчивается с уходом на анод всех возникших  электронов, причем большая часть электронов и соответственно ионов очевидно возникла вблизи анода. Примем в качестве упрощающего допущения, что все ионы возникли вблизи анода и обозначим через t время дрейфа ионов от анода до катода. Время дрейфа электронов существенно меньше, и им пренебрежем. Эмиссия электронов в момент времени t происходит под действием тех ионов, которые возникли в момент времени t-t

i_e(t) = i₀ + mi_e(t-t) = i₀  + m(i_e(t) - tdi_e/dt)

Отсюда получаем

mtdi_e/dt = i₀ + (m-1)i_e(t)

Разделяем переменные

 

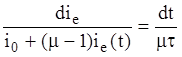
Умножим обе части на (m-1) и добавим под знак дифференциала i₀

                   

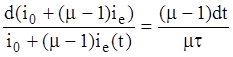
Интегрируя от 0 до t получаем

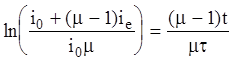
Берем экспоненту от обеих частей и умножаем на mi₀

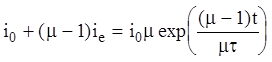
Собираем члены содержащие i₀  справа и делим на m-1

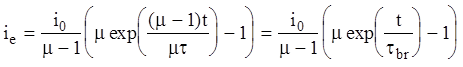
где  введено характерное время пробоя

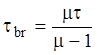
С увеличением перенапряжения t уменьшается а m увеличивается и таким образом время развития пробоя уменьшается, требуется меньшее число последовательных лавин, чтобы ток вышел на стационарное значение. Поскольку каждая лавина несколько расплывается в поперечном направлении, то даже если развитие разряда началось с одного электрона, постепенно разряд охватывает весь объем промежутка и плотность тока не меняется в поперечном направлении, если не считать конечно краевых эффектов. Токи протекающие через промежуток в Таунсендовском разряде порядка наноампера или микроампера.

7. Предельный ток Таунседовского разряда. При уменьшении R или при увеличении ЭДС ток пропускаемый через промежуток растет, возрастает плотность заряженных частиц и они начинают искажать внешнее поле. Давайте рассмотрим этот процесс.Сначала получим распределение зарядов в промежутке в нулевом приближении, считая Е = U/d. Запишем еще раз уже рассматривавшуюся систему уравнений

dj_е/dx =aj_e

dj_i/dx = -aj_e

j = j_e + j_i

но уже не будем считать, что из катода эмиттируется какой-то начальный ток и таким образом граничные условия следующие:

j_е(0) = gj_i(0)

j_i(d) = 0

Уравнения легко интегрируются и используя граничные условия получаем

j_e =

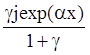
j_i =

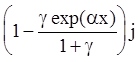
Поскольку g << 1 то в большей части промежутка j_i  превышает j_e и близок к j. Кроме того, поскольку скорость дрейфа ионов на два порядка меньше скорости дрейфа электронов, то можно сделать вывод, что практически во всем промежутке, за исключением очень малой прианодной области преобладает ионный заряд. Положим

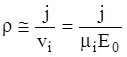
и определим чему равно электрическое поле в первом приближении

Е(х) = Е₀  + Е₁(х),

Решаем уравнение Пуассона

dE₁/dx = -r_i/e₀  = -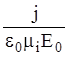

Интегрируя получаем

E₁(x) - E₁(0) = -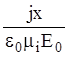

Напряженность электрического поля линейно уменьшается с ростом х. Существенное искажение внешнего поля произойдет, когда добавка станет величиной того же порядка, что и Е₀. Положим

E₁(0) - E₁(d) = 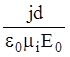 ~  Е₀

Отсюда получаем оценку сверху для предельной плотности тока таунсендовского разряда

j_m  ~ 

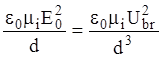
8. Переход от таунсендовского разряда к тлеющему. При j  ~  j_m  поле в промежутке существенно отличается от постоянного. Но тогда и к-т a не будет постоянной величиной и условие самостоятельности, одной из форм записи которого является соотношение

ad = ln(1/g + 1), следует видоизменить

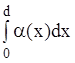= ln(1/g + 1)

Поскольку зависимость a(х) = a(Е(х)) является достаточно сложной функцией, то довольно трудно сказать к чему приведет искажение поля, к увеличению или уменьшению напряжения необходимого для самоподдержания разряда, либо наконец уменьшение и увеличение поля и к-та a в разных точках промежутка в точности компенсируют друг друга и напряжение не измениться. Для того чтобы проанализировать возможное развитие ситуации разложим к-т a в ряд в окрестности точки Е₀ 

a(Е(х)) = a(Е₀) + a'(Е₀)(Е(х)-Е₀) + a''(E₀)(E(x) - E₀)²/2

и проинтегрируем

a(Е₀)d + a'(Е₀)(U - U_br) + a''(E₀)ò((E(x) - E₀)²/2)dх = ln(1/g + 1)

Учитывая, что

a(Е₀)d = ln(1/g + 1)

получаем

a'(Е₀)DU + a''(E₀)S = 0

где DU = U - U_br, S = ò((E(x) - E₀)²/2)dх

Производная a' всегда положительна