Источники поверхностного типа. Поверхностная адсорбция. Плотность ионного тока, страница 2

В результате целого ряда тщательно проведенных экспериментов Тейлору и Ленгмюру удалось определить число атомов цезия в заполненном монослое (3,56-10¹⁴ см^{— 2}) и величину 6 — степень покрытия — для любой скорости поступления цезия на поверхность и температуры вольфрама. Им удалось установить связь между величиной работы выхода и значением 9 и зависимость скорости испарения с поверхности атомов и ионов, а также скорости электронной эмиссии от степени покрытия и температуры. Результаты экспериментов приводятся ниже в том виде, как это сделано в работе Форрестера [91]. Скорости атомной и ионной эмиссии — v_p и v_a соответственно — представляют собой число частиц, испаряющихся с площади 1 см² за 1 с. Оба эти параметра могут быть написаны в виде

v=exp(A-B/T)                                                                          (9.6)

где Т — абсолютная температура, а А и В — функции θ, различные, естественно, для атомов и ионов. Для атомов имеем соотношения

A_a=61+4,8(θ- θ²)+ln []+(9.7)

и

B_a=32380/(1+0,7140)                                                                       (9.8)

В случае ионной эмиссии

   А_р=А_а-ln2                                                                             (9.9)

и

B_p=B_a-8681+11606V_c                                                               (9.10)              

где V_c — контактная разность потенциалов между чистым вольфрамом и поверхностью, покрытой цезием, т. е. величина, на которую происходит снижение работы выхода вольфрама в результате возникновения на его поверхности цезиевого покрытия.

Измерения этой величины были проведены Тейлором и Ленгмюром. Результаты измерений были представлены в виде таблицы. В работе [91] определяется (методом наименьших квадратов) полином четвертого порядка, наилучшим образом проходящий через эти экспериментальные точки, и показано, что контактная разность потенциалов может быть представлена в виде

V_c= 10,6790 — 22,9829² + 42,53е^з — 34,919⁴,                                (9.11)

что хорошо укладывается в пределы ошибок измерений.

Изотермическая кривая скорости испарения как функции 9, представленная на рис. 9.2, может быть построена исходя из уравнений (9.6) — (9.11). Такая кривая ведет себя более сложным образом, чем можно было бы ожидать. Выход ионов возрастает до своего максимального значения при 9~0,01 и затем резко падает. Атомный выход устойчиво возрастает с ростом 9, но при 6 = 0,01 он настолько мал по сравнению с ионным выходом, что полная скорость испарения достигает максимума практически при том же значении 0, при котором ионный ток максимален.

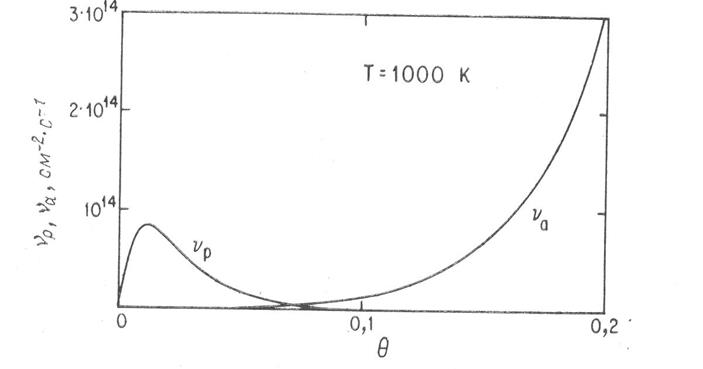
Рис. 9.2. Зависимость скорости испарения ионов v_p и атомов v_a при отсутствии внешнего электрического поля и температуре поверхности 1000 К от степени покрытия.

Это свидетельствует о скачкообразном характере зависимости плотности ионного тока с вольфрамовой поверхности от скорости поступления на поверхность цезия. Представим, например, что пары цезия поступают на нагретую до 1000 К поверхность вольфрама со скоростью, медленно нарастающей от нуля до значения 8,5-10¹³ атом/(см²-с). При этом θ будет нарастать до значения 0,012, и испаряющийся цезий будет практически на 100% ионизован. Дальнейшее незначительное увеличение скорости поступления цезия уже не будет сопровождаться малым приращением θ. Скорее произойдет неизбежное скачкообразное нарастание значения θ до величины ~0,156, при таком значении испарение происходит исключительно в виде нейтралов.

Полезно отметить, что в пределе очень малых θ уравнения (9.6) —(9.11) дают

v_p=θ exp(61,31-23699/T)                                                                (9.12)

9.3. Плотность ионного тока

Тогда как параметр θ полезен для общего понимания явления поверхностной ионизации, зависимость плотности ионного тока J_p=ev_p от температуры с фракцией нейтралов в качестве параметра (рис. 9.3) позволяет успешно использовать эффект