Обобщающие уроки по теме «Величины», страница 2

в) 4 сут. + 48 ч, 48 ч = 2 сут.        4 сут. + 2 сут. = 6 сут.

г) 6 мин - 359 с, 6 мин = 360 с, 360 - 359 = 1 (с) 

д)32 ч + 16ч =48 ч = 4 сут.

3. Установи правило, по которому записа­ны величины в первых двух столбцах, и по этому же правилу запиши величины в третьем столбце:

15 м                    63 т 500 кг                     2 сут. 12 ч

150 дм                635 ц

1500 см               63 500 кг    

15 000 мм           63 500 000 г       

Дети замечают, что в столбцах каждая сле­дующая величина выражается в более мелких единицах по сравнению с предыдущей: в пер­вом столбце метры выражаются в дециметрах, дециметры - в сантиметрах, сантиметры – в миллиметрах; во втором столбце тонны – в центнерах, центнеры - в килограммах, кило­граммы - в граммах.

Чтобы составить третий столбец, надо за­писанную величину выразить сначала в часах, затем в минутах, потом в секундах:

2  сут. 12 ч

            60 ч

3 600 мин

            216 000 с

4.         Луноход прибыл на Луну в 10 ч 10 мин. Когда был произведен запуск, если продолжи­тельность полета составила 1 ч 15 мин?

Дети записали решение двумя способами:

1-й способ

1) 10 ч 10 мин- I ч 10 мин = 9 ч

2) 9 ч -5 мин = 8 ч 55 мин

2-й способ

1) 10 ч 10 мин = 610 мин

2) 1 ч 15 мин = 75 мин

3) 610 мин - 75 мин = 535 мин

4) 535 мин : 60 мин = 8 ч 55 мин

Устанавливается, какой способ рациональ­нее и почему.

5.         Исследование длилось с 10 ч 15 мин до 12 ч 45 мин. Каждые полчаса информация от­правлялась на Землю. Сколько раз принимали информацию в центре управления полетом?

Решая данную задачу, у детей закрепляется умение переводить однородные величины, вы­раженные в единицах одних наименований в другие:

1)        12 ч 45 мин - 10ч 15 мин = 2 ч 30 мин - длилось исследование

2)        2 ч 30 мин : 30 мин, 2 ч 30 мин = 150 мин,  150: 30 = 5 (раз)

Ответ: информацию в ЦУП принимали 5 раз.

6.         Полет продолжался 3 ч. Дополните каж­дую величину до трех часов:

а) 145 мин,     б) 139 мин,    в) 170 мин. Это задание учащиеся выполняют двумя способами: 1) переводят часы в минуты или 2) выражают минуты в более крупных единицах. Выполняя задание а) первым способом, дети рассуждают так: «Чтобы узнать, сколько часов в 145 мин, надо 145 разделить на 60, получим 2 ч 25 мин, 3 ч - 2 ч 25 мин = 35 мин. Или по-другому: 3 ч - это 180 мин, 180 - 145 =35 мин».

Аналогично рассуждая, учащиеся записы­вают два способа решения и для других вели­чин:

б)        139 мин = 2 ч 19 мин, 3 ч-2 ч 19 мин = 41 мин,  180- 139 = 41 (мин)

в)         170 мин = 2 ч 50 мин, 3 ч - 2 ч 50 мин = 10 мин, 180- 170= 10 (мин)

Обобщение знаний о соотношении единиц величин осуществляется при выполнении дей­ствий с величинами, выраженными в единицах двух наименований. Эту работу можно органи­зовать по-разному.

Приведем фрагмент урока, на котором обобщались знания о величинах.

1. На доске вывешены карточки с записан­ными на них величинами:

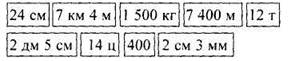
Предлагается перевернуть все карточки об­ратной стороной и прочитать: «Том и Джерри».

Дается задание найти лишнюю карточку ве­личин. (Лишняя карточка 400 - это число, а не величина.) Оставшиеся карточки разделить на две группы и расположить в порядке убывания.

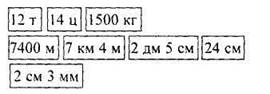
Учитель говорит: «Сегодня на уроке мы бу­дем в роли мультипликаторов и попробуем со­чинить новую серию про Тома и Джерри». На доске вывешены кадры из мультфильма.

Кадр 1. Джерри в магазине

Том отправил Джерри в магазин за продук­тами, намекнув, чтобы он купил для него боль­ше любимой еды, чем для себя. Но хитрая мышь сделала наоборот. Масса каких продук­тов больше? На сколько граммов масса смета­ны меньше массы крупы? Во сколько раз мас­са сыра больше массы сосисок?

Сосиски-150 г           Сметана - 250 г

Сыр - 3 кг        Крупа - 1 кг 500 г

Отвечая на первый вопрос, учащиеся срав­нивают массу крупы и сметаны, выполнив действие вычитания: 1 кг 500 г - 250 г = 1 кг 250 г.

Давая ответ на второй вопрос, выполняют действие деление: 3 кг = 3000 г, 3000 : 150 = 20 (раз).

Дети  говорят: «Джерри  купил  крупы  на 1 кг 250 г больше, чем сметаны, а сыра в 20 раз больше, чем сосисок».

Кадр 2. Сборы

 Собираясь на рыбалку, Том отмотал для удочки 12 м 94 см лески. Но Джерри тайком отрезал от лески Тома для своей удочки кусок такой длины, что у Тома осталось 763 см лес­ки. Сколько денег сэкономит Джерри, если I см лески стоит 2 к.?

Дети записывают решение самостоятельно.

Одни из них записали так:

1) 12 м 94 см = 1 294 см

2) 1294 см - 763 см = 531 см

3) 2*531 = 1 062 (к.) = 10р. 62 к.

Ответ: 10 р. 62 к. сэкономил Джерри.

Другие выполнили действия так:

1)  763 см = 7 м 63 см

2)  12 м 94 см - 7 м 63 см = 5 м 31 см

3)  5 м 31 см = 531 см

4)  2*531 = 1 062 (к.) = 10р. 62 к.

            Ответ: 10 р. 62 к. сэкономил Джерри.

Сравнивая решения, устанавливают, какое из них рациональнее и почему.

Кадр 3. Наживка для рыбы

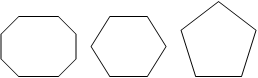Том заранее решил нарыть червей и выкопал несколько ямок следующей формы:

Проводится беседа:

-  В виде каких геометрических фигур изо­бражены ямки? (В виде многоугольников.)

-  Установите закономерность в построении геометрических фигур. (Так как здесь изобра­жены  правильные  многоугольники:   восьми­угольник, семиугольник, шестиугольник, пя­тиугольник, значит, следующим должен быть квадрат.)

-  Чему равна сторона квадрата, если его площадь 81 м²? (9 см.)

-  На сколько квадратных сантиметров уве­личится площадь квадрата, если его сторону увеличить на 1 см? (На 19 см².)

-  Поясните, как рассуждали. (Если сторону квадрата увеличить на 1 см, то она будет равна 10 см, тогда площадь квадрата 100 см². Чтобы узнать,  на сколько  квадратных  сантиметров увеличится площадь квадрата, надо из 100 см² вычесть 81 см², получится 19 см².)

Кадр 4. Улов

На доске текст задачи: «Том и Джерри при­шли на озеро ловить рыбу. У Тома в ведре ры­бы больше, чем в котелке у Джерри. Хитрая мышь положила в ведро еще 1 кг 200 г рыбы, а в котелок 3 кг 350 г. Где рыбы стало больше и на сколько?»

Учащиеся замечают, что в данном тексте задачи не хватает данных. Карточка со словами «больше» переворачивается обратной стороной, на которой записано: «Больше на 2 кг 300 г».

Дети по тексту задачи составляют схему и записывают решение:

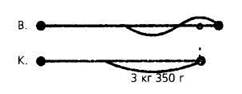
1 кг 200 г 2 кг 300 г     ^;

1) 2 кг 300 г + 1 кг 200 г = 3 кг 500 г

2)3 кг 500 г - 3кг 350 г = 150 г

Ответ: в ведре на 150 г рыбы больше.

Одним из важнейших критериев результа­тивности обучения является не только сформированность у учащихся знаний математических понятий, но и умение применить их в различных условиях. Подтверждением этому служат зада­чи, составленные детьми по заданию учителя: продолжить историю Тома и Джерри, придумав свои версии для героев мультфильма.

Приведем в качестве примера некоторые сюжеты, продолжающие мультфильм.

Аня Е. Ужин Тома и Джерри.

Джерри съел на 300 г рыбы меньше, чем Том. Сколько весит один окунь, если Джерри съел 4 одинаковых окуня, а Том 6 таких же окуней? Сколько килограммов рыбы они съели вместе?

1-й способ

1)6-4 = 2 (ок.) - весят 300 г

2) 300 : 2 = 150 (г) - масса одного окуня

3) 150 • 4 = 600 (г) - съел Джерри

4) 150 • 6 = 900 (г) - съел Том

5) 600 + 900 = 1 500 (г) - съели вместе

2-й способ

1)300 : 2 = 150 (г) - масса одного окуня

2)150 • 10 = 1 500 (г) - съели Том и Джер­ри вместе

Ответ: масса 1 -го окуня 150 г. Том и Джерри съели 1 кг 500 г рыбы.

Марина К. Том и Джерри пловцы.

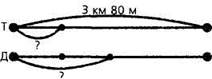
Том и Джерри одновременно поплыли от одного берега к другому. Расстояние между бе­регами 3 км 80 м. Том проплыл это расстояние за 1 ч 10 мин, а Джерри в 2 раза быстрее. Сколько метров проплывал за 1 минуту Том и сколько метров проплывал за 1 минуту Джер­ри? На сколько метров больше проплывал за 1 минуту Джерри?

1)1 ч 10 мин = 70 мин

2)3 км 80 м = 3080 м

3) 3080 : 70 = 44 (м/мин)

4)44 • 2 =88 (м/мин)

5)88 - 44 = 44 (м/мин)

Ответ: скорость Джерри больше на 44 м/мин.

Формирование общего подхода к изуче­нию математических понятий позволяет уча­щимся переосмысливать изучаемый матери­ал, самостоятельно ориентироваться в нем, использовать его в разных ситуациях. Об этом свидетельствуют приведенные приме­ры задач с величинами, составленные уча­щимися.