Оптимальная и квазиоптимальная фильтрация последовательностей радиоимпульсных сигналов, страница 3

где - несущая частота задерживаемых колебаний.

     Если, например, T=1 мс, N=20 и t=1 мкс, то t_з=0,019 с, число отводов –18, полоса – 2 МГц, а нестабильность   .

     Столь высокие требования к стабильности задержки задерживающего устройства и его элементов объясняются тем, что в рассматриваемом фильтре должно происходить синфазное сложения колебаний, которое могут нарушить температурные нестабильности устройства задержки. Поэтому для нормальной работы фильтра нестабильности должны быть намного меньше периода колебаний несущей частоты.

      В оптимальных фильтрах для последовательности видеоимпульсов требования к стабильности элементов задержки значительно более легкие. Так как сложение импульсов происходит на видеочастоте, то для нормального функционирования фильтра достаточно взаимного временного перекрытия суммируемых импульсов, что выполняется при условии: , где - длительность суммируемых импульсов, которая имеет порядок микросекунды. Однако выполнение даже этого условия требует принятия специальных мер по стабилизации времени задержки задерживающего устройства путем его термостатирования.

2. Квазиоптимальная фильтрация.

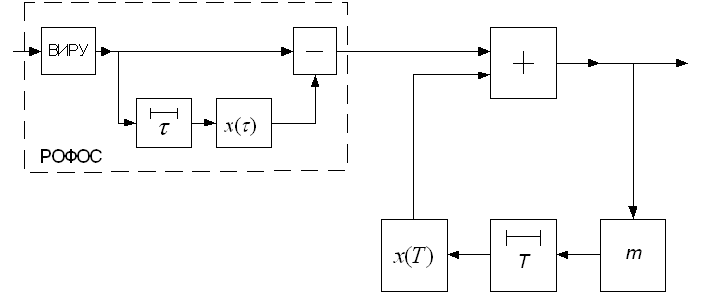
      Несколько упрощается реализация устройства когерентной обработки последовательности радиоимпульсов, если заменить идеальный радиочастотный накопитель радиочастотным рециркулятором (рис.5), так как в этом случае устройство задержки выполняется на время Т и не имеет дополнительных отводов.

Рис.5. Структурная схема квазиоптимальной фильтрации последовательностей радиоимпульсных сигналов.

  Однако осуществление и такого устройства с нестабильностями, много меньшими периода несущего колебания, - весьма сложная и практически невыполнимая задача.

      В этом и заключается главный недостаток оптимальных фильтров для когерентных последовательностей радиоимпульсов и вообще фильтрового метода их оптимальной обработки.