Разобьем выборку на 10 интервалов, вероятность попадания в каждый из которых равняется 10%:
{[0; 2.1072), [2.1072; 4.4629), [4.4629; 7.1335), [7.1335; 10.2165), [10.2165; 13.8629) ,
[ 13.8629; 18.3258), [18.3258; 24.0795), [24.0795; 32.1888), [32.1888; 46.0517), [46.0517; ∞)}
 Количество случайных величин, попавших в каждый интервал
равно соответственно:
Количество случайных величин, попавших в каждый интервал
равно соответственно:
[21 21 24 13 14 27 14 20 23 20]
«Хи квадрат» подсчитанный для данной выборки равен 9.8500. Это значение оказывается меньше значения χ29, 0.05 = 16.91898, так что можно считать данную выборку распределенной по экспоненциальному закону. А значит и генератор построен корректно.
![]()
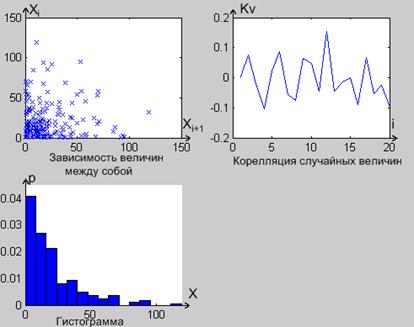
 По
графику зависимости каждой последующей величины от предыдущей и графику
корелляции можно говорить о том, что величины между собой независимы. Для
подтверждения соответствия сгененрированных случайных величин экспоненциальному
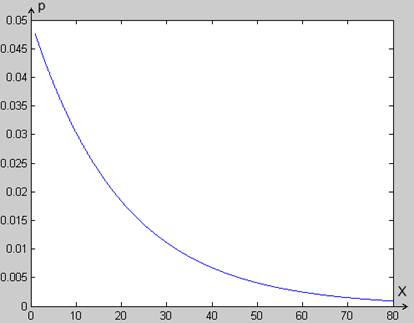
распределению наглядно, можно использовать гисторамму. Гистограмма
характеризует плотность распределения случайной величины. Видно, что
гистограмма на Рисунке 2 соответствует искомой плотности распределения (Рисунок
1). Значит генератор построен правильно, и создаваемые им случайные величины
соответствуют экспоненциальному распределению.
По
графику зависимости каждой последующей величины от предыдущей и графику
корелляции можно говорить о том, что величины между собой независимы. Для
подтверждения соответствия сгененрированных случайных величин экспоненциальному
распределению наглядно, можно использовать гисторамму. Гистограмма
характеризует плотность распределения случайной величины. Видно, что
гистограмма на Рисунке 2 соответствует искомой плотности распределения (Рисунок
1). Значит генератор построен правильно, и создаваемые им случайные величины
соответствуют экспоненциальному распределению.
Для дискретной случайной величины, характеризующей приоритет поступаемых заявок, сначала нужно задать таблицу
распределения. Для удобства зададим каждому приоритету числовое значение – наименьший = 1, наивысший = 5. Считаем, что большинство заявок имеет приоритет, выставляемый системой по умолчанию и равный 3. Это соответствует действительности, так как пользователь их просто добавляет в систему. Однако, имеются некоторые файлы, которые он хотел бы получить раньше других, и те, которые ему нужны как можно раньше. Обычно соотношение их с общим числом поступающих заявок на закачку составляет 13% и 7% соответственно. Кроме того, имеются файлы, которые вполне можно закачать после всех остальных. Их обычно 10% от общего числа. Ну и, наконец, пользователь добавляет и такие файлы, которые просто хотел бы иметь у себя, но время, через которое они закачаются, его совершенно не волнует. Процент таких файлов (с наименьшим приоритетом) составляет 5%.
Таким образом случайной величине приоритета соответствует следующая таблица распределения:
Таблица2. Распределение случайной величины приоритета.
|
Значение приоритета |
1 |
2 |
3 |
4 |
5 |
|
Вероятность, % |
5 |
10 |
65 |
13 |
7 |
Генератор дискретной случайной величины основан на генераторе стандартной равномерно распределенной величины. Листинг такого генератора приведен ниже:
1 function X = gener_discr( g1, n, a )
2 k1 = 630360016;
3 k2 = 2147483647;
4 s = size(a);
5 r(1) = k1*g1;
6 while (r(1) > k2 ),
7 r(1) = r(1)/k2;
8 end
9 for i=2:1:(n+1)
10 r(i) = mod(k1*r(i-1), k2);
11 r(i-1) = r(i-1)/k2;
12 for j=1:1:(s(2))
13 if ( sum(a(2,1:j-1)) <= r(i-1) )&&( r(i-1) <= sum(a(2,1:j)) )
X(i-1) = a(1, j);
break;
14 end
15 end
16 end
17 end
В данной функции первый параметр – начальное значение генератора, второй – количество случайных величин, которые нужно сгенерировать, третий – таблица распределения случайной величины.
Оценим корректность данного генератора критерием «хи квадрат». Для этого с помощью генератора получена выборка из 200 значений случайной величины, приведенная ниже:
Таблица 3. Выборка 200 значений дискретной случайной величины.
|
1 |
3 |
4 |
5 |
3 |
4 |
2 |
3 |
|
4 |
3 |
3 |
3 |
5 |
5 |
3 |
3 |
|
3 |
4 |
3 |
3 |
3 |
4 |
3 |
3 |
|
3 |
4 |
5 |
3 |
5 |
2 |
3 |
3 |
|
4 |
3 |
2 |
3 |
3 |
3 |
3 |
3 |
|
1 |
2 |
4 |
5 |
4 |
2 |
3 |
3 |
|
3 |
3 |
2 |
3 |
3 |
3 |
2 |
3 |
|
3 |
2 |
3 |
3 |
4 |
4 |
3 |
2 |
|
3 |
3 |
4 |
3 |
5 |
4 |
3 |
1 |
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
4 |
|
3 |
3 |
4 |
3 |
1 |
3 |
3 |
3 |
|
4 |
3 |
3 |
3 |
2 |
3 |
3 |
3 |
|
3 |
5 |
3 |
3 |
1 |
3 |
3 |
3 |
|
2 |
4 |
3 |
3 |
3 |
3 |
4 |
4 |
|
1 |
3 |
3 |
2 |
3 |
3 |
3 |
2 |
|
3 |
1 |
2 |
3 |
3 |
3 |
3 |
1 |
|
3 |
2 |
3 |
3 |
3 |
4 |
3 |
4 |
|
3 |
3 |
3 |
5 |
3 |
5 |
4 |
3 |
|
Таблица 3. Выборка 200 значений дискретной случайной величины (продолжение). |
|||||||
|
3 |
4 |
3 |
3 |
3 |
3 |
3 |
2 |
|
3 |
4 |
3 |
3 |
3 |
3 |
3 |
3 |
|
1 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
|
1 |
3 |
4 |
2 |
3 |
4 |
3 |
4 |
|
3 |
4 |
3 |
2 |
3 |
2 |
3 |
3 |
|
4 |
3 |
3 |
3 |
4 |
3 |
3 |
3 |
|
3 |
2 |
1 |
3 |
3 |
3 |
1 |
3 |
Выборка была разбита на интервалы {[0; 1], (1; 2], (2; 3], (3; 4], (4, 5]}.
Вероятность попадания в каждый из них равна соответственной 5%, 10%, 65%, 13% и 7%.
![]() В каждый
интервал попало 12, 21, 127, 30 и 10 величин соответственно.
В каждый
интервал попало 12, 21, 127, 30 и 10 величин соответственно.
«Хи квадрат» в данном случае равен 0.4500, что меньше значения χ24, 0.05 = 9.48773. Таким образом генератор является достоверным.
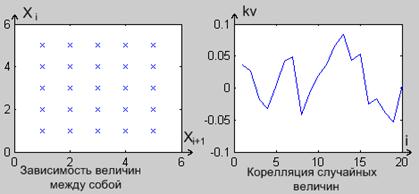
![]() По
графикам корелляции (Рисунок 3) можно говорить о независимости генерируемых
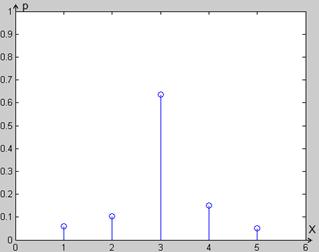
величин между собой. Соответствие графика плотности распределения (Рисунок 4)
таблице распределения дискретной случайной величины доказывает корректность
генератора.
По
графикам корелляции (Рисунок 3) можно говорить о независимости генерируемых
величин между собой. Соответствие графика плотности распределения (Рисунок 4)
таблице распределения дискретной случайной величины доказывает корректность
генератора.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.