



Лекция 6
6.1. Определение дифференциального сечения рассеяния с заданной энергией
атома отдачи и полного сечения рассеяния
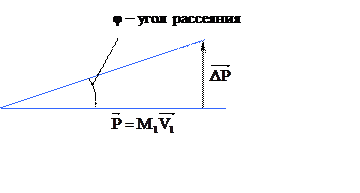
Рассмотрим атом M2, бомбардируемый ионами M1. Те ионы, которые проходят через площадь 2πpdp, заключенную между окружностями радиусом p и p+dp, рассеиваются в интервале углов φ, φ + dφ. Величину
dσ = 2πpdp, (6.1)
равную вышеуказанной площади, называют дифференциальным сечением взаимодействия (в данном случае рассеяния). Уравнение (5.13) (см. лекцию 5) при известном потенциале V(r) позволяет выразить p2 через φ. Дифференцируя получаем 2pdp, т.е. фактически связь между dσ и dφ откуда с использованием уравнения (3.19) (E2=ΛE1sin2φ/2, см. лекцию 3) определяем сечение dσ столкновений с энергией атома отдачи в интервале dЕ2.
Полное
сечение рассеяния для Е2, принимающего значения в
интервале от ![]() до
до ![]() , может
быть получено интегрированием
, может
быть получено интегрированием
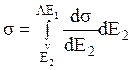 . (6.2)
. (6.2)
Вероятность приобретения атомом отдачи энергии в интервале Е2, Е2 + dЕ2 есть, очевидно, отношение дифференциального сечения к полному:
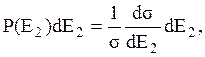 (6.3)
(6.3)
где 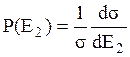 –
плотность вероятности.
–
плотность вероятности.
Выразить интеграл (5.13) для угла рассеяния φ (как функции p2) через аналитические функции возможно лишь для простых потенциалов (таких. как кулоновский и 1/r2). В других случаях должны применяться численные методы решения уравнения (5.13). В связи с этим полезно рассмотреть два приближенных расчета.
Когда φ достаточно мало, а это значит, частицы проходят друг от друга относительно далеко, т.е., прицельный параметр Р относительно велик. Скорость частиц при этом существенно не меняется. Траектории частиц близки к прямым линиям (почти прямые линии).
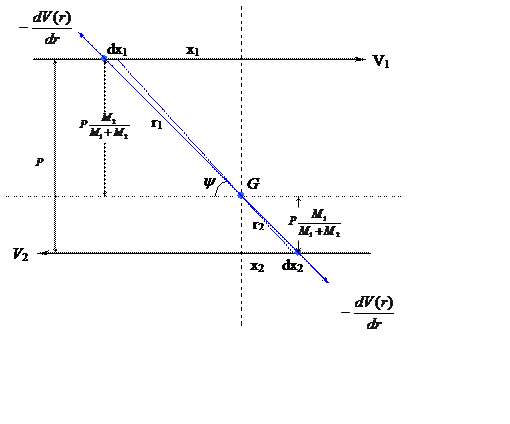
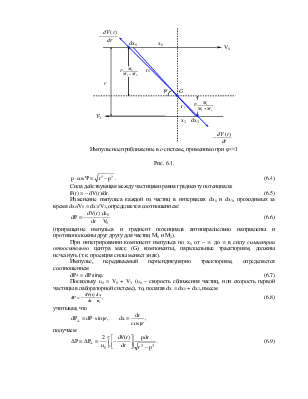
Импульсное приближение в c-системе, применимо при φ<<1
Рис. 6.1.
![]() . (6.4)
. (6.4)
Сила действующая между частицами равна градиенту потенциала:
F(r) = – dV(r)/dr. (6.5)
Изменение импульса каждой из частиц в интервалах dx1 и dx2, проходимых за время dx1/V1 = dx2/V2, определяется соотношением:
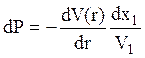 (6.6)
(6.6)
(приращение импульса и градиент потенциала антипараллельно направлены и противоположны друг другу для частиц М1 и М2).
При интегрировании компонент импульса по х1 от – ∞ до ∞ в силу симметрии относительно центра масс (G) компоненты, параллельные траекториям, должны исчезнуть (т.к. проекция силы меняет знак).
Импульс, передаваемый перпендикулярно траекториям, определяется соотношением
dP┴ = dP sinφ. (6.7)
Поскольку u1 = V1 + V2 (u1 – скорость сближения частиц, или скорость первой частицы в лабораторной системе), то, полагая dx = dx1 + dx2, имеем
![]() , (6.8)
, (6.8)
учитывая, что
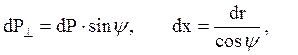
получаем
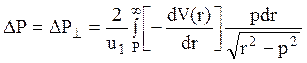 . (6.9)
. (6.9)
tg φ ≈ φ
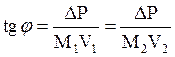
Обозначим через I(p) интеграл (6.9), тогда
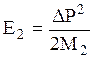 ,
, 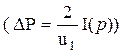 (6.10)
(6.10)
Значение ΔР=ΔР^ не зависит от выбора системы координат (лабораторная или
с-система) и, поскольку 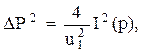 то
то
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.