Осколки деления. Первичные атомы отдачи и тяжелые ионы. Быстрые электроны. Релятивистские столкновения

Лекция 8

8.1.Осколки деления

Тяжелое ядро урана 235 асимметрично расщепляется на 2 части с общей энергией 160 МэВ. Наиболее вероятна ситуация, когда получаются два осколка с энергиями и массами Е₁ = 95 МэВ, М₁ = 96 а.е.м. и Е₂ = 55 МэВ, М₂ = 137 а.е.м. В качестве грубого приближения можно взять кулоновский потенциал 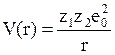. Это оправданно лишь при , т.е., соударениях, близких к лобовым (тогда dσ, Р(Е₂) и  то же, что и для быстрых легких ионов (см. предыдущую лекцию), а именно:

.                                     (8.1)

При более низких энергиях Р(Е₂) будет менее чувствительно к изменению Е₂. Точный расчет дает, что при малых Е₂: .

 

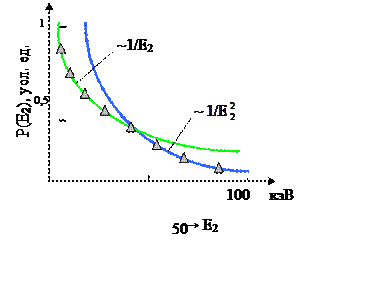Рис. 8.1. Функция P(E₂) для осколков деления (точки – эксперимент).

8.2. Первичные атомы отдачи и тяжелые ионы (E < 10⁶ эВ)

Для первичных атомов отдачи здесь мы будем применять индекс 1 (сделаем замену: 2 → 1). Атомы отдачи образуются при облучении внутри вещества, а дальше мы их изучаем как тормозящиеся мишенью ускоренные частицы отдачи с индексом 1. При таком разъяснении недоразумений не возникает. Из рисунка 6.1, представленного в предыдущей лекции (кривая 3), видно, что для тяжелых ионов с Е < 10⁶ эВ подходит обратноквадратичный потенциал. В дальнейшем мы рассмотрим более точную теорию Линхарда-Шарфа-Шиотта, использующую несколько видоизмененный потенциал. Сейчас же сделаем предварительные оценки.

Потенциал r^–2 справедлив  для области . Точное решение уравнения траекторийдает для 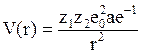 следующий результат:

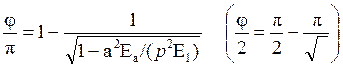                          (8.2))

где Е_а = Е₁ при ρ₀ = а 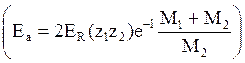. Последнее соотношение следует из (4.14), (4.18) и (5.16). Тогда с использованием соотношения  получаем

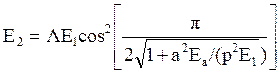                                       (8.3)

Выражая p² из этого уравнения через Е₂ и дифференцируя 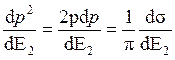, получаем

 

(8.4)

где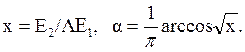

При малых х, т.е., малых Е₂ это выражение приобретает вид:

 

(8.5)

Это приближение очень хорошее при x < 1 (E₂ < ΛE₁) и, следовательно, его можно использовать практически на всем интервале возможных энергий атомов отдачи от 0 до ΛE₁. Результаты расчета приведены на рисунке.

 

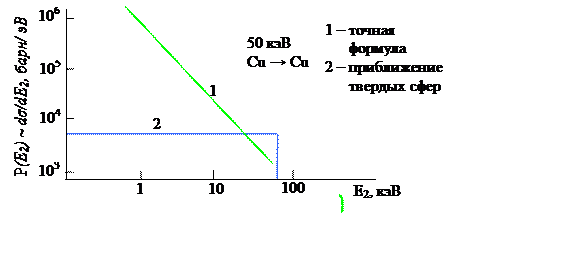Рис.8.2. Сечения взаимодействия для ионов Cu (50 кэВ), тормозящихся в Cu (1 – точная формула (8.4) и приближенная формула (8.5), 2 – приближение твердых сфер)

Барн – ядерная площадь для описания ядерного сечения: 1 барн = 10^–24 см². Из соотношения (7.13), так же, как и на прошлой лекции, можно найти, что

                                                           (8.6)

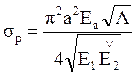                                                       (8.7)

Как будет далее показано для тяжелых атомов с Е₁ = 50 кэВ, пробег в матрицах, состоящих также из тяжелых атомов, составляет ~ 10³ Å (0,1 мкм). Согласно (8.6)= 1 кэВ. Следовательно, всего будет ~ 50 радиационных повреждений (до полной потери энергии) на длине 0,1 мкм. Т.е., среднее расстояние между нарушениями L = 10³ Å/50 = 20 Å .

8.3. Быстрые электроны. Релятивистские столкновения

 

Так как М₂ >> M₁=m (где m – масса электрона), то процессы в с- и l-системах практически совпадают. Нас интересуют энергии, необходимые для создания радиационных повреждений: E ~ m₀c² ≥ 0,5 МэВ. Следовательно, мы имеем дело с релятивистскими энергиями и скоростями. Процессы квантовые (это мы отмечали ранее). Достаточно сложен вопрос о потенциале.

Здесь                                          P₁ = mu₁                                                                                                            (8.8)

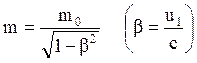                                                       (8.9)

                                              (8.10)

Передаваемый импульс

                                                       (8.11)

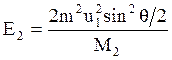,                                                           (8.12)

тогда

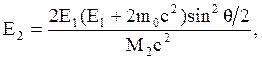                              (8.13)

откуда максимально возможная энергия отдачи при θ = π

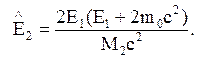                                           (8.14)

Приближенное решение уравнения Дирака для легких элементов получено Мак-Кинли и Фишбахом:

      (8.15)

где  Это выражение является точным по членам, содержащим β² и αβ. При малых β оно приближается к закону рассеяния Резерфорда.

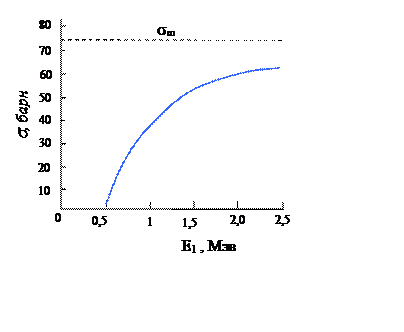
Рис.8.3. Сечение образования нарушения в меди ()

 

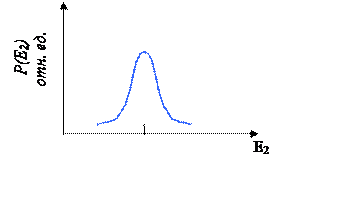
Рис. 8.3. Функция P(E₂)=(1/σ)(dσ/dE₂) – острый максимум вблизи .

 

(8.16)

Таблица 8.1.

Свойства атомов отдачи, образующихся при различных видах излучений  (М₂ = 50)

Частица	Расстояние между первичными ионами (атомами) отдачи, см	Длина траектории частицы, см	Средняя энергия атома отдачи, эВ	Распределение атомов отдачи по энергиям Р(Е2)
Протон, 1МэВ	10–3	10–3	200
Осколок деления, 100 МэВ	10–7	10–4	103	при высоких энергиях  при низких энергиях
Тяжелый ион, 50 кэВ	10–6	10–5	7·103	Примерно
Электрон, 1 МэВ	0,1	0,1	5,0·104	Пик вблизи
Нейтрон, 2 МэВ	5	100	1,6·105	, все энергии равновероятны
Нейтрон (спектр реактора на тепловых нейтронах)	5	100	104	Примерно  при низкой энергии, более быстрый спад при высокой энергии