Столкновение ионов и атомов. Общее теоретическое рассмотрение траекторий при столкновении

Лекция  5

5. Столкновение ионов и атомов

5.1. Общее теоретическое рассмотрение траекторий при столкновении.

Мы показали, что для частиц с M > m_p при энергиях 10⁴–10⁷ эВ, представляющих интерес с точки зрения радиационных повреждений, пригодна классическая механика (т. е. можно пренебречь волновыми свойствами частиц и релятивистскими поправками). В частности, мы можем говорить о траекториях.

Изобразим траектории столкновения двух частиц в с-системе с прицельным параметром P* и координатами частиц  и (или (r₁, Ψ) и (r₂, Ψ) – в полярных координатах).

в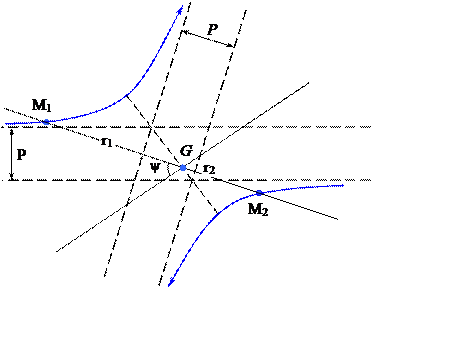

Траектория сталкивающихся частиц в с-системе

Рис. 5.1.

Поставим задачу об отыскании вероятности того, что частица массой М₂ будет иметь энергию отдачи в интервале от Е₂ до Е₂+dЕ₂ в l-системе, т.е., об отыскании величины Р(Е₂)dЕ₂ (где Р(Е₂) – соответствующая плотность вероятности).

Сначала детально рассмотрим траектории, чтобы выразить φ как функцию P, E₁, V(r), M₁ и M₂. Нормальная и касательная  составляющие скорости М₁ есть  и , а полная скорость  – .

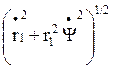Выражение для полной скорости М₂ аналогично: .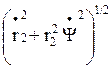

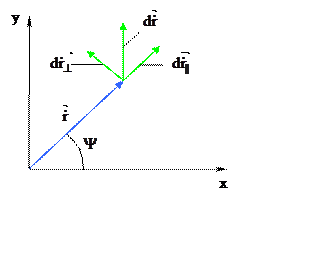
Составляющие скорости:  - параллельная,  - касательная

Рис. 5.2.

При упругом столкновении сумма потенциальной и кинетической энергии должна быть равна асимптотической сумме E кинетических энергий. Поскольку

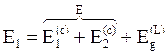,                                                (5.1)

то 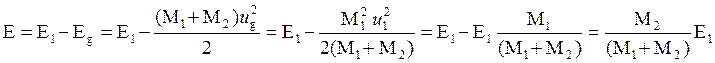   (5.2)

– и, следовательно,

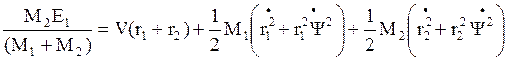.                 (5.3)

Учитывая, что

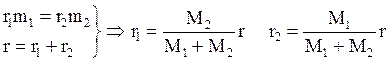,                           (5.4)

получаем: 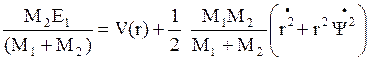                             .                        (5.5)

Выражение в скобках можно преобразовать к виду

	(5.6)

 

 

Кроме закона сохранения механической энергии, должен соблюдаться закон сохранения момента количества движения или момента импульса (mvr), а значит, в любой точке траектории момент импульса должен быть равен его асимптотическому значению

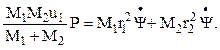                           (5.7)

Учитывая соотношения (5.4)

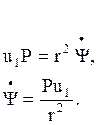имеем                                                                                                                (5.8)

Вводя обозначение  и подставляя в (5.5), получаем

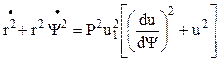.                                      (5.9)

Уравнение (5.3) для энергий при этом примет вид:

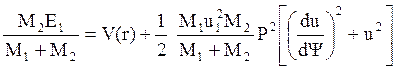,                          (5.10)

упрощая которое: 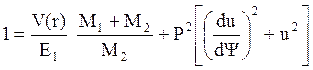                ,                               (5.10, a)

получаем 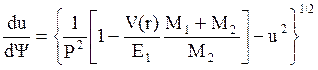                              .                              (5.11)

Как можно видеть, в последнем выражении уже нет зависимости от времени. Это и есть уравнение траекторий. Угол рассеяния находится отсюда, если выразить dΨ как функцию u и du и взять интеграл по первой ветви траектории.

Значение Ψ  при этом изменяется от φ/2 до π/2.

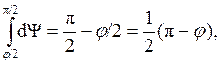                                                   (5.12)

откуда

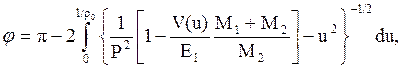                          (5.13)

где ρ₀ – значение r при 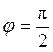, т.е., расстоянии максимального сближения (или минимальное расстояние между частицами).

Так как 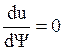при 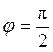, значение ρ определяется из соотношения для

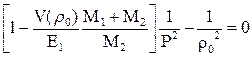                                            (5.14)

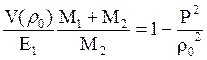                                                     (5.15)

	.

 

(5.16)

С учетом последнего соотношения, выражение (5.13) дает искомую зависимость φ от P.