I.Данные
Вид искомой передаточной функции — Y21 (далее Y(P) ):
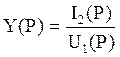
Схема активного четырехполюсника — схема №2
Величина сопротивления обратной связи — вариант г:
![]() кОм
кОм
Используемые параметры транзистора — H
Номер транзистора — 1:
H11=200 Ом H12=2∙10-4 H21=30 H22=10-4 См
Схема пассивного четырехполюсника — №1
Вариант исходных данных для пассивного четырехполюсника — вариант б:
L=10-5 Гн C=0.5∙10-9 Ф R=12 Ом
Полная схема четырехполюсника:
II. Расчет передаточной функции четырехполюсника
Для упрощения расчетов заменим транзистор схемой замещения с заданными параметрами H, далее заменим транзисторный каскад эквивалентным генератором.
1. Расчет UХХ
![]() кОм
кОм
H11=200 Ом
H12=2∙10-4
H21=30
H22=10-4 См
Запишем уравнения методом узловых потенциалов
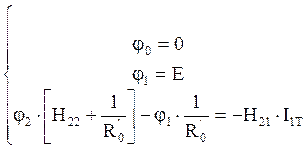
Учитывая что ![]() =UХХ
, из последнего уравнения получим:
=UХХ
, из последнего уравнения получим:
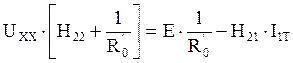 (1)
(1)
Запишем второй закон Кирхгофа для 1 контура:
I1T∙H11=E – H12∙ U2Т
Учитывая что U2T=UХХ получим:
I1T=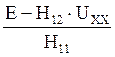 (2)
(2)
Подставляя (2) в (1) получим:
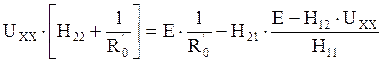
Выражая UХХ через Е получим:
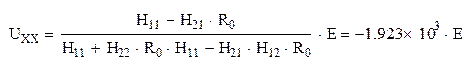
2. Расчет IКЗ и RГ
Составим уравнения Кирхгофа:
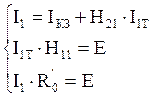
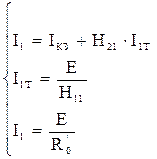
Подставляя последние 2 уравнения в первое получим:
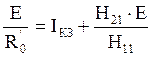
Отсюда
IКЗ=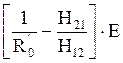 = –0.15∙E
= –0.15∙E
Тогда сопротивление эквивалентного генератора:
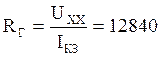 Ом
Ом
3. Расчет передаточной функции:
Y(P)=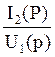
E1=UХХ= –1923∙E
RГ=12820 Ом
R=12 Ом
L=10-5 Гн
C=5∙10-10 Ф
Перейдем к операторной схеме
Рассчитаем ток I2(P)
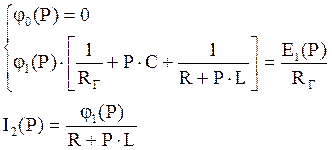 (1)
(1)
Выражая в уравнении (1) ![]() через E1(P) и подставляя в последнее уравнение, получим:
через E1(P) и подставляя в последнее уравнение, получим:
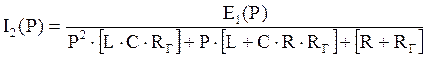
Y(P)=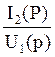 =
= 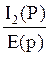 =
=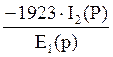
Тогда
Y(P)= 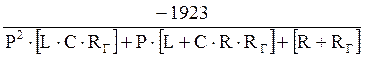
С подставленными значениями:
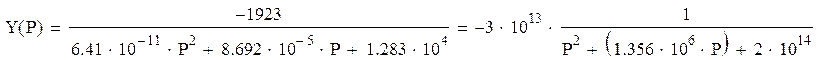
Полюсы передаточной функции:
P= –6.78∙105 ± 1.413∙107 ∙ j
Резонансная частота:
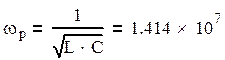
III.Частотные характеристики четырехполюсника
1. Расчет по передаточной функции
H(j∙w)=Y(j∙w)
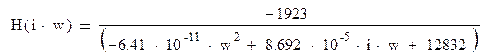
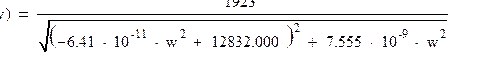
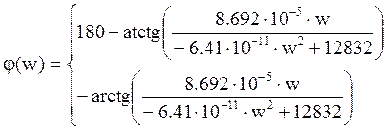
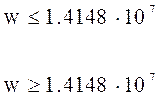
2. Расчет по карте нулей и полюсов
H(w)=3∙1013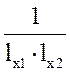
|
w |
lx1∙107 |
lx2∙107 |
H(w) |
|
0 |
1,414 |
1,414 |
0,15 |
|
0.5∙wр |
2,135 |
0,707 |
0,1987 |
|
wр |
2,828 |
0,0707 |
1,5 |
|
1,5∙wр |
3,549 |
0,721 |
0,10948 |
|
∞ |
∞ |
∞ |
0 |
![]()
|
w |
φx1 |
φx2 |
φ (w) |
|
0 |
85 |
-85 |
180 |
|
0.5∙wр |
87 |
-82 |
175 |
|
wр |
88 |
0 |
92 |
|
1,5∙wр |
88 |
81 |
11 |
|
∞ |
90 |
90 |
0 |
IV. Временные характеристики четырехполюсника
1. Расчет импульсной характеристики g(t)
Импульсная характеристика g(t) есть обратное преобразование Лапласа от передаточной функции: g(t)=Y(P).
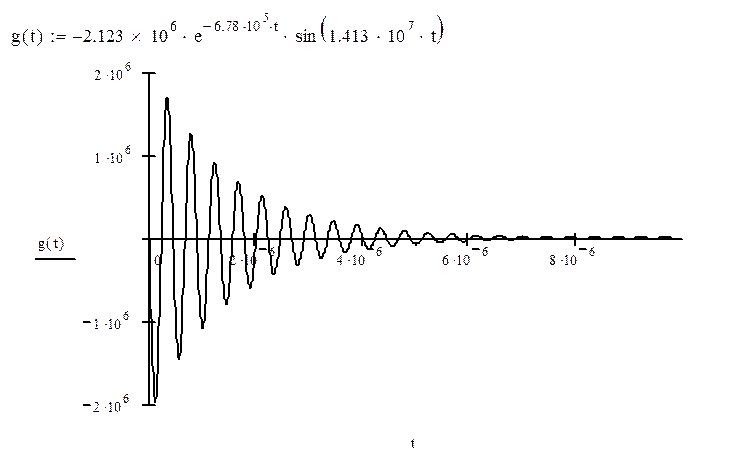
2. Расчет переходной характеристики h(t)
Переходная характеристика h(t) есть
обратное преобразование Лапласа от передаточной функции, деленной на P : h(t)=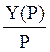 .
.
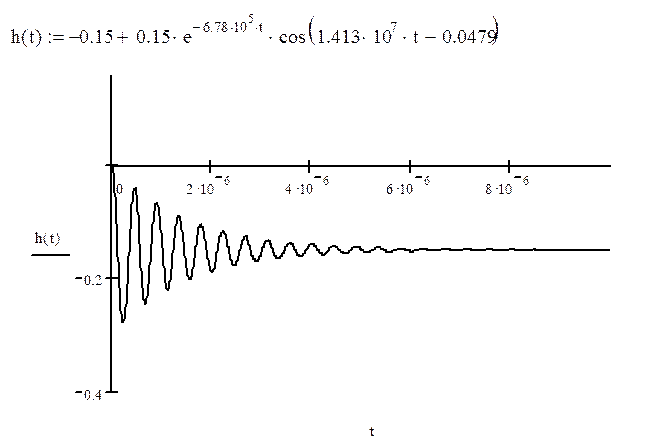
3. Проверка соответствия временных характеристик друг другу
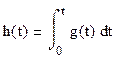
Раскроем косинус разности в выражении h(t):
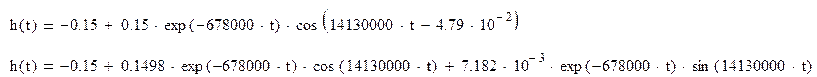
Проинтегрируем g(t) от 0 до t:
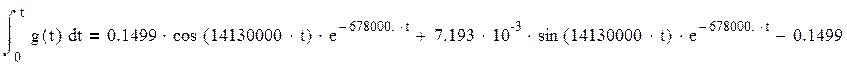
Сравнивая это выражение с последним выражением для h(t) и учитывая погрешности вычислений заключаем что:
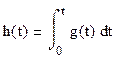
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.