Расчет схемы активного четырехполюсника. Определение АЧХ и ФЧХ по карте нулей и полюсов

ЗАДАНИЕ

Порядковый номер в журнале: 24.

Искомая передаточная функция: .

Схема активного четырехполюсника: 1.

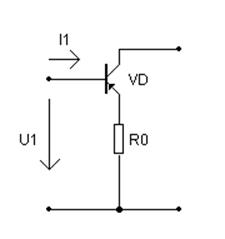
 (Ом).

Номер транзистора: 3.

Параметры транзистора: .

 (См),               

 (См),

 (См),

 (См).

Схема пассивного четырехполюсника: 24.

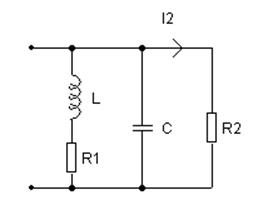
 (Гн),

(Ф),

(Ом),

(Ом),

Таким образом, расчетная схема имеет вид:

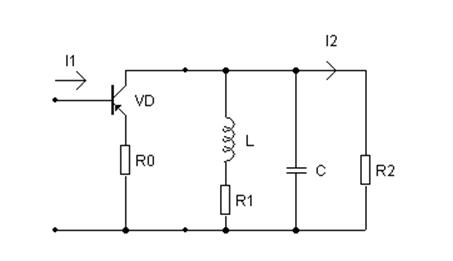
Искомая передаточная функция: .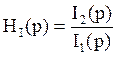

Тогда для упрощения расчетов на вход надо подключить источник тока. Имеем схему:

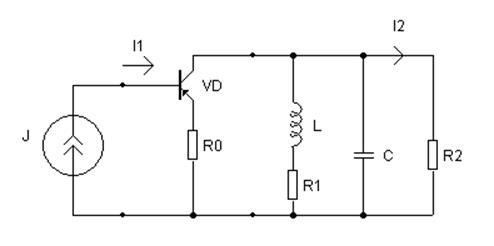
Применим метод эквивалентного генератора, генератором объявим следующую часть схемы:

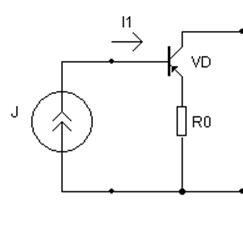
Заменим транзистор его эквивалентной схемой. Схема, объявленная генератором, примет вид:

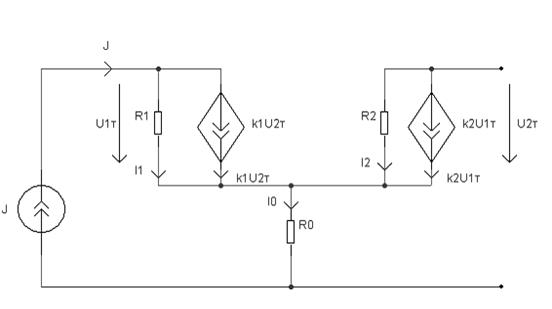
Здесь:

,

,

,

,

.

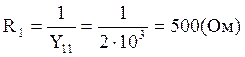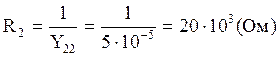Найдем для этой схемы .

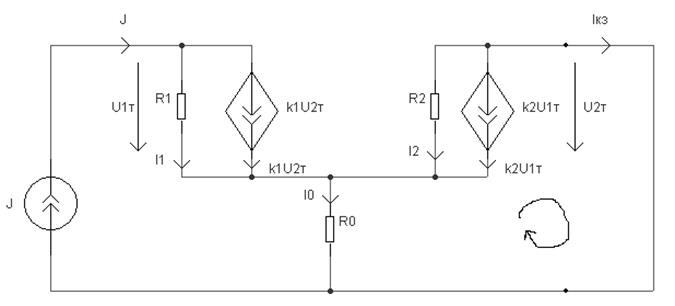
Запишем систему уравнений по Кирхгофу:

.

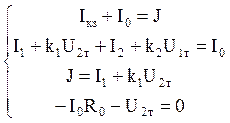Учитывая, что  , , система уравнений примет вид:

.

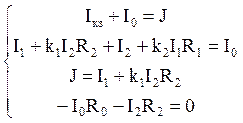Находить все токи и напряжения не имеет смысла. Найдем только . Выражение для  будет иметь вид:

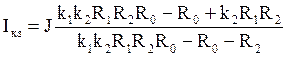
Подставляя численные значения , получим:

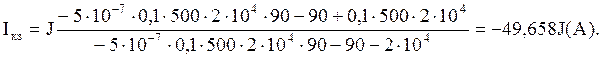
Найдем .

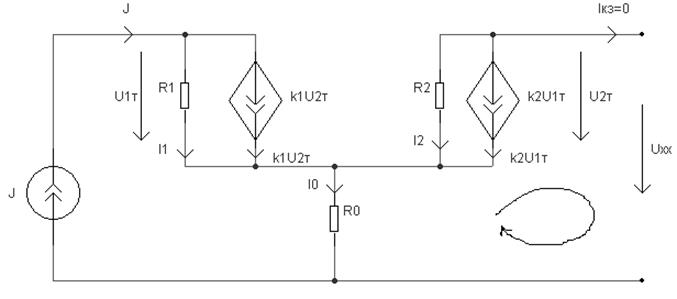
Запишем систему уравнений по Кирхгофу:

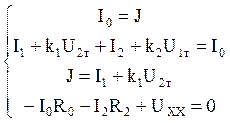
Учитывая, что  , , система уравнений примет вид:

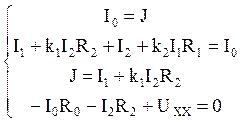
Находить все токи и напряжения не имеет смысла. Найдем только. Выражение для  будет иметь вид:

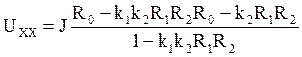
Подставляя численные значения , получим:

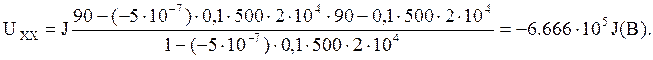
Найдем :

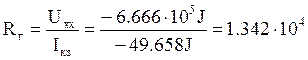(Ом).

Составим схему с эквивалентным генератором:

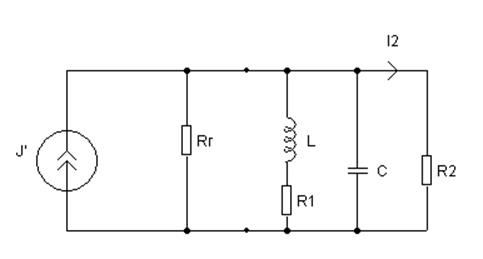
Здесь .

Найдем ток  операторным методом, учитывая нулевые начальные условия.

Составим операторную схему:

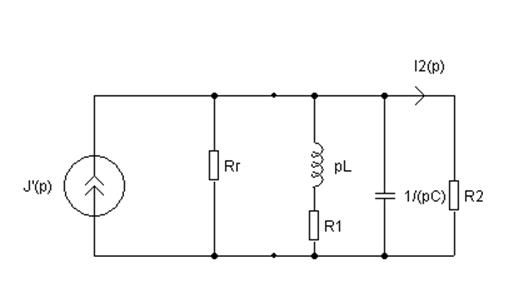
Здесь .

Свернем схему.

Изобразим полученную схему:

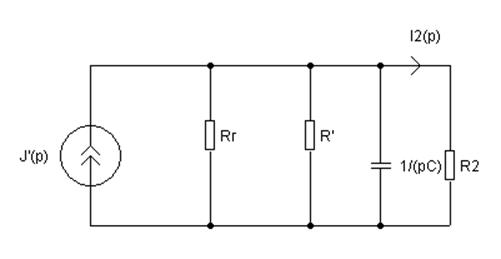
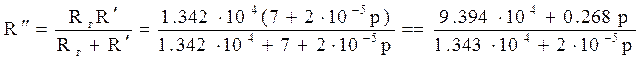
Изобразим полученную схему:

.

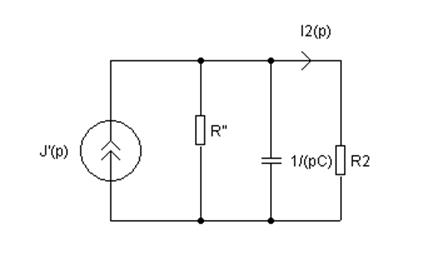
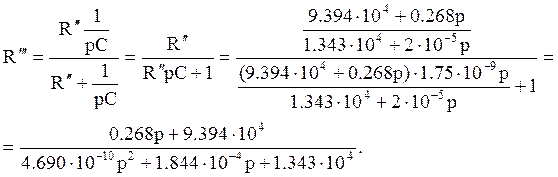Изобразим полученную схему:

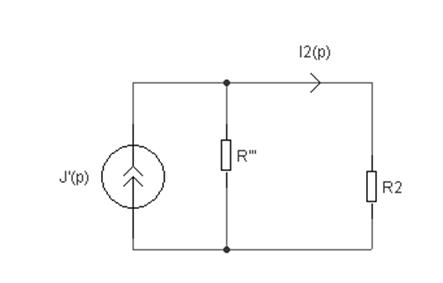
По формуле распределения токов имеем:

 ,

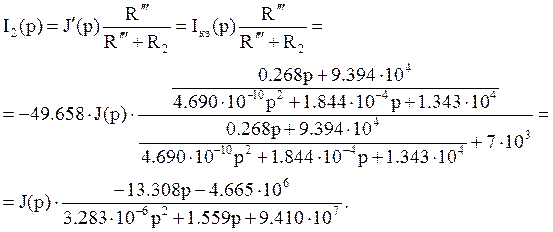
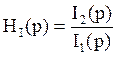Тогда передаточная функция будет выглядеть так:

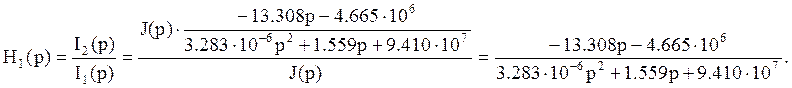
Масштабный множитель равен отношению коэффициентов при старших степенях.

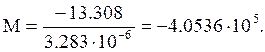
Найдем нули передаточной функции:

Данное уравнение имеет один действительный корень:

Найдем полюсы передаточной функции:

.

Данное уравнение имеет два комплексно-сопряженных корня:

По найденной передаточной функции найдем переходную характеристику  и импульсную характеристику .

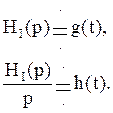
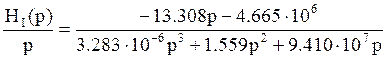
Проверим найденные выражения для  и .

Преобразуем  и  к виду:

.

Вынесем  общий множитель за скобки. Получим:

В соответствии с тригонометрическими формулами:

 где 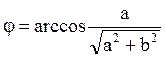 ,   получим:

 если угол  выражен в радианах,

, если угол  выражен в радианах,

По полученной передаточной функции для расчетной схемы  найдем АЧХ и ФЧХ.

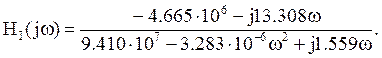
Найдем АЧХ.

                                

        

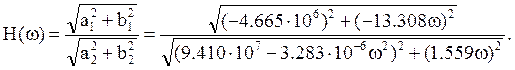
Найдем ФЧХ.

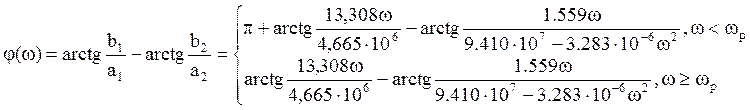
Здесь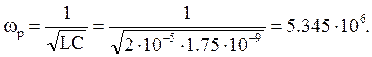

Построим карту нулей и полюсов.

Найдем АЧХ и ФЧХ по карте нулей и полюсов.

АЧХ.

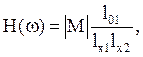
где М - масштабный множитель.

ФЧХ.

Масштабный множитель отрицательный, поэтому имеем формулу:

Измерения будем проводить в точках: , , ,  , .