Сумма трёх слагаемых равна 69. Первое слагаемое равно 24, а второе на 17 больше первого? ______________________________________________
3. Дополните условие задачи так, чтобы данных было достаточно для её решения:
Мама дала на ужин папе 2 булочки, а сыну - одну. Сколько булочек съела за ужином вся семья?
4. Придумайте задачу, которую можно решить с помощью уравнения, и запишите её условие: 24 + X + (24 - 8) = 55.
Комплект№3. Вариант 1.
1. Составьте выражение для решения задачи:
а) Участники велогонок в первый день проехали 187 км, а во второй день - А км. Сколько километров они проехали за два дня?
б) На станке в час можно изготовить 7 деталей. Сколько деталей можно изготовить на этом станке за “А” часов?
2. Проанализируйте примеры и сформулируйте правила, которые подтверждают эти примеры:
а) 3 • 21 = 3 • (20+1 ) = 3 • 20 + 3 • 1 = 60 + 3 = 63;
17 • 52 = 17 • (50 + 2) = 17 • 50 + 17 • 2 = 850 + 34 = 884;
б) 5 + 2 - 2 = 5 + (2 - 2) = 5 + 0 = 5;
20 + 7 - 7 = 20 + (7 - 7) = 20 + 0 =20;
в) 70 : 2 • 2 = (70 : 2) • 2 = 35 • 2 =70;
90 : 11 • 11 = (99 : 11) • 11 = 9 • 11 = 99.
3. Определите закономерность и продолжите ряд чисел:
а)1,3,9,27,... б) 5,10,9,14,...
4. Какие из следующих фигур могут быть развёрткой куба?
а) б) в) г) д) е) ж) ...
5. Лошадь живёт до 35 лет, а собака до 20 лет. На сколько лет лошадь живёт дольше собаки?
Составьте задачу с вопросом: “Сколько лет живёт лошадь?”
6. Составьте задачу, которую можно решить с помощью уравнения:
а) X + 3 = 5; б) 4 • У = 56;
7. Сумма каких четырёх однозначных чисел равна их произведению?
Вариант 2.
1. Составьте выражение для решения задачи:
а) Поезд находиться в движении 5 часов, а потом ещё “а” часов. Сколько всего времени поезд находится в движении?
б) Масса кирпича 3 кг. Сколько весят “в” таких кирпичей?
2. Проанализируйте примеры и сформулируйте правила, которые подтверждают эти примеры:
а) 4 • 17 = 4 • (20 - 3) = 4 • 20 - 4 • 3 = 80 - 12 = 68;
15 • 29 = 15•(30 - 1)=15•30 - 15•1= 450 -15=435;
б) 31 – 4 + 4= (31 - 4) + 4 = 31
519 - 50 + 50 = (519 - 50) + 50 = 469 + 50 = 519;
в) 34 • 5 : 5 = (34 • 5): 5 = 170 : 5 = 34;
41• 2:2 = (41• 2) : 2 = 82 : 2=41.
3. Определите закономерность и продолжите ряд чисел:
а)1,2,3,4,8,... 6)5,15,6,14,...
4. Какие из следующих фигур могут быть развёрткой куба?
а) б) в) г) д) е) ж) ...
5. Лошадь живёт до 35 лет, а собака до 20 лет. На сколько лет лошадь живёт дольше собаки?
Составьте задачу с вопросом: “Сколько лет живёт собака?”
6. Составьте
задачу, которую можно решить с помощью уравнения:
а) 7 + Х=14; б) У• 2 = 24.
7. Какое однозначное число равно сумме своих делителей, отличных от него самого?
Результаты исследования. По совершению обработки результатов исследования проводится оценивание каждого учащегося по 10 пунктам: 7 пунктов выделено в структуре МС; данная диагностика дополняется рейтинговой оценкой каждого учащегося учителем начальной школы, учителем, ведущим экспериментальные занятия в классе, самооценкой самого учащегося. На основании анализа результатов диагностики составляется рейтинговый лист учащихся по каждому классу; кроме того, может быть составлена диаграмма сравнения результатов выполнения учащимися класса заданий структуры МС (например, с целью выработки рекомендаций по совершенствованию методической работы учителя начальной школы в процессе обучения математике).
По результатам исследования выделяется четыре группы учащихся:
СМ - малоспособные к математике - учащиеся этой группы с большим трудом понимают объяснения учителя, испытывают трудности при выполнении примеров и задач; приёмы аналогового мышления у них развиты слабо, уровень навыка устного счёта низкий, их отличают также повышенная утомляемость на уроке;
СР - средние способности к математике - характеризуются достаточной хорошими успехами в обучении математике за счёт многократного повторения каждого конкретного приёма решения примера или задачи, хорошо развиты приёмы аналогового мышления, навык устного счёта, но такой учащийся испытывает, как правило, трудности при переходе к новым типам задач;
С - способные к математике - такие учащиеся без усилий овладевают новыми приёмами мыслительной деятельности, предлагают собственные оригинальные решения задач, свободно вычисляют устно;
ОС - очень способные к математике - учащиеся отдают предпочтение математике среди других учебных дисциплин, занимаются самостоятельно, сюда обычно включают и все характеристики группы С.
Предлагаем таблицу, отражающую результаты конкретного измерения математических способностей учащихся:
Распределение учащиеся по математическим способностям
|
Группа |
Количество учащихся, классы (%) |
Всего |
||
|
ОС С СР СМ |
||||
Рейтинговые листы измерения способностей являются анонимными и хранятся в документах администрации.
По результатам диагностического исследования строится диаграмма развития математических способностей учащихся по семи названным выше критериям:
РАЗВИТИЕ МАТЕМАТИЧЕСКИХ СПОСОБНОСТЕЙ УЧАЩИХСЯ
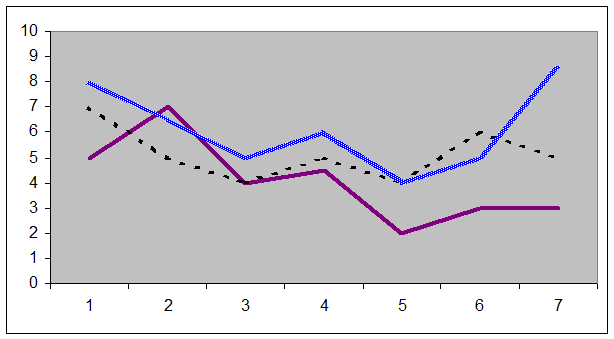
В данной диаграмме:
ОХ - Критерии математических способностей;
ОУ - Уровни развития математических способностей (по результатам выполнения заданий).
По оси ОХ откладываются пункты структуры МС; по оси ОУ - средний по классу результат выполнения задания соответствующей диагностики, для удобства чтения преобразованный по формуле: средний в %10.
Ранняя диагностика позволяет более точно, целенаправленно разработать педагогическую стратегию и тактику дальнейшего развития математических способностей особо одарённых учащихся вплоть до формирования профильных математических классов. К ним относится: разработка индивидуальных заданий по математике повышенной сложности, привлечение в кружок юных математиков, к участию в математических олимпиадах и т.д.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.