Парная регрессия. Определение параметров линейного уравнения регрессии, страница 2

Формула для нахождения:

Ᾱ =  ⋅100%

4.1. Для линейного уравнения регрессии:

Ᾱ =  ⋅ 0.931 ⋅ 100% = 6.208% - средняя ошибка аппроксимации показывает хорошее соответствие фактического значения издержек на производство продукции(у) и выравненного значения издержек на производство продукции(ŷ),  то есть качество модели хорошее.

4.2. Для степенного уравнения регрессии:

Ᾱ =  ⋅ 0.963 ⋅ 100% = 6.422% - средняя ошибка аппроксимации показывает хорошее соответствие фактического значения издержек на производство продукции(у) и выравненного значения издержек на производство продукции(ŷ),  то есть качество модели хорошее.

Задание 5:

Чтобы с вероятностью 0.95 оценить значимость каждого параметра уравнений регрессии (линейного и степенного), необходимо использовать t-критерий Стьюдента:

1.  Сначала необходимо определить t_табл:

α = 1-0.95 = 0,05

df – число степеней свободны = n-m-1 = 13

Значит, t_табл = 2,160

2.  Найти среднюю (стандартную) ошибку оцениваемых параметров по формулам:

Se(a) =

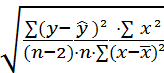
Se(b) =  

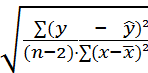
Se(r ) = 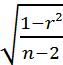   используется только для линейного уравнения.

3.  Рассчитать фактическое значение t-критерия для каждого параметра по формуле:

t_i =  , где i – параметр

4.  Сравнить |t_i|  и t_табл, оценить значимость параметра.

5.1. Для линейного уравнения регрессии:

Se(a) =  = 0.430                  t_a =  = 23.435         |t_a| ≥ t_табл

Se(b) =  = 0.027                        t_b =  = 6.492            |t_b| ≥ t_табл

Se(r ) =  = 0.135                           t_r =  = 6.492           |t_r| ≥ t_табл

Значит, параметры a, b и r значимы с вероятностью 0.95.

5.2. Для степенного уравнения регрессии:

Для нахождения средних ошибок параметров, необходимо использовать линеаризованную форму степенного уравнения регрессии: Ŷ=2.058+0.188⋅Х

Se(a) =  = 0.087                        t_a =  = 23.753               |t_a| ≥ t_табл

Se(b) = 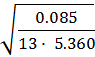 = 0.035                            t_b =  = 5.380                |t_b| ≥ t_табл

Значит, параметры а и b значимы с вероятностью 0,95.

Чтобы с вероятностью 0,95 проверить значимость каждого уравнения регрессии (линейного и степенного), необходимо использовать F-критерий Фишера:

1.  Сначала необходимо определить F_табл:

α = 1- 0.95 = 0.05

df₁ = m = 1

df₂ = n-m-1 = 13

Значит, F_табл = 4,667

2.  Найти фактическое значение F-критерия:

Для линейного уравнения регрессии: F = t_b² = t_r²

Для степенного уравнения регрессии: F =

3.  Сравнить F и F_табл, оценить значимость уравнения.

5.3. Для линейного уравнения регрессии:

F = 6.492² = 42.153

F≥F_табл, значит линейное уравнение регрессии статистически значимо с вероятностью 0,95. Его можно использовать для прогнозов.

5.4. Для степенного уравнения регрессии:

F =  = 28.948

F≥F_табл, значит степенное уравнение регрессии статистически значимо с вероятностью 0,95. Его можно использовать для прогнозов.

Задание 6:

Чтобы выбрать лучшее из двух полученных уравнений регрессии и сравнивать их, необходимо проверить, значимы ли параметры этих уравнений. Согласно пунктам 5.1. и 5.2. это условие выполняется. Сами уравнения также являются значимыми согласно пунктам 5.3. и 5.4.

После этого необходимо сравнить коэффициенты детерминации линейного и степенного уравнений регрессии:

·  Для линейного уравнения регрессии: R² = 0.764

·  Для степенного уравнения регрессии: R² = 0.690

Так как у двух полученных уравнений одинаковое количество параметров, то лучшим будет то, у которого R² больше. В данном случае коэффициент детерминации больше у линейного уравнения регрессии, значит,  будет лучшим уравнением из двух полученных.

Задание 7:

В предыдущем задании я выбрала линейное уравнение регрессии как лучшее, значит, по нему с вероятностью 0,95 необходимо построить доверительный интервал ожидаемого значения издержек на производство продукции в предположении, что среднее время простоя оборудования уменьшится на 8% от среднего по совокупности.

Для этого, в первую очередь, надо найти прогнозируемое время простоя оборудования. Оно будет считаться по формуле:

_пр = 0.92 ⋅

Подставлю известные значения: _пр = 0.92 ⋅ 13.4 = 12.328 дней

После этого найду значение издержек на производство продукции, найденное при заданном _пр по линейному уравнению регрессии , то есть проведу точечный прогноз.

ŷ_пр = 10.077 + 0.175 ⋅ 12.328 = 12.239 млн.руб.

Так как фактические наблюдения не лежат на линии регрессии, а рассеянны вокруг нее, то возникает необходимость найти границы этого рассеивания для заданного _пр , то есть провести интервальный прогноз по формуле:

_табл ⋅ Se(ŷ_пр)

Для этого необходимо найти Se(ŷ_пр) по формуле:

Se(ŷ_пр) =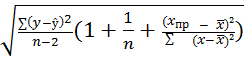

Подставлю известные значения: Se(ŷ_пр) =  = 0.929

После этого можно искать доверительный интервал, значит:

_ниж = 12.239 – 2.160 ⋅ 0.929 = 10.232 млн.руб.

_верх = 12.239 + 2.160 ⋅0.929 = 14.245 млн.руб.

С вероятностью 0,95 ожидаемое значение издержек на производство продукции находится в границах от 10.232 млн.руб. до 14.245 млн.руб.

Чтобы проверить надежность данного расчета, можно посчитать следующий показатель:

D =  =  = 1.392 раза

Выполненный расчет оказался надежным и точным с вероятностью 0.95, так как диапазон верхней и нижней границ доверительного интервала составляет 1.392 раза.