Парная регрессия. Определение параметров линейного уравнения регрессии

Министерство образования и науки РФ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА СТАТИСТИКИ

КОНТРОЛЬНАЯ ТОЧКА № 1

по учебной дисциплине «Эконометрика»

На тему:

«Парная регрессия»

Вариант 20

Выполнила:

Михайлова Ольга Владимировна

3 курс

Специальность: экономика –

бухгалтерский учет, анализ и аудит

Э-316

Научный руководитель: 

Бороздина Ольга Юрьевна

Санкт-петербург

2013

Дано:

Таблица 1

Предприятие	Издержки на производство продукции, млн руб.	Среднее время простоя оборудования, дней
	y	x
1	10,3	5
2	10,5	12
3	10,6	5
4	10,7	10
5	11	7
6	11,5	5
7	12	13
8	12,2	7
9	12,5	18
10	12,6	9
11	13	10
12	13,9	18
13	14,4	19
14	15,2	27
15	16	36

Решение:

Задание 1:

В таблице 1 представлены статистические данные об издержках на производство продукции и среднем времени простоя оборудования для 15 предприятий. Требуется проанализировать зависимость издержек на производство продукции от среднего времени простоя оборудования.

В соответствии с этим первый показатель будет результирующим признаком, который обозначу у, а другой будет фактором, и его обозначу соответственно х.

По заданию 1 необходимо построить поле корреляции, значит, на оси абсцисс будут лежать значения фактора - среднего времени простоя оборудования; на оси ординат – значения результата - издержек на производство продукции.

График 1 «Поле корреляции»

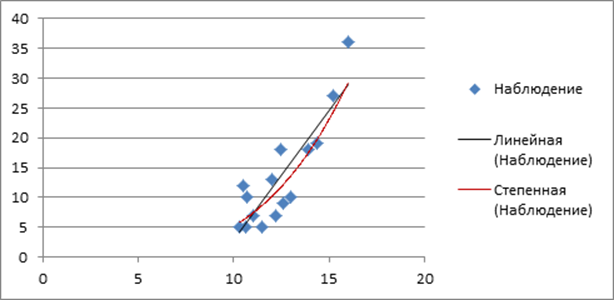
Каждая отмеченная точка – это исходное значение наблюдений издержек на производство продукции и среднего времени простоя оборудования. Эти значения и есть фактические (или наблюдаемые) значения результата и  фактора.

Задание 2:

2.1. Для линейного уравнения регрессии:

Чтобы определить параметры линейного уравнения регрессии, необходимо использовать метод наименьших квадратов(МНК):

Подставлю известные значения:

Получаю:a=10.077

b=0.175

Значит, линейное уравнение регрессии имеет вид . С увеличением среднего времени простоя оборудования на 1 день издержки на производство продукции увеличатся в среднем на 0.175 млн.руб.

Значение параметра а=10,077 говорит о том, что при отсутствии простоя оборудования издержки на производство продукции в среднем равны 10,077 млн.руб.

2.2. Для степенного уравнения регрессии:

Чтобы определить параметры степенного уравнения регрессии, его необходимо привести к линейной форме, то есть провести их линеаризацию.

Степенное уравнение:

Пусть, ln(y)=Y

ln(x)=X

ln(a)=A

Тогда, линеаризованное уравнение имеет вид: Y=A+b⋅X

Значение b находится по формуле:

b =  =

Подставляю известные значения:

b = = 0.188

Значение параметра А находится по формуле:

А =  + b⋅ = 2.511+0.188⋅2.412=2.058

Линеаризованное уравнение имеет вид Ŷ=2.058+0.188⋅Х

Чтобы перейти к исходному уравнению регрессии – степенному, его необходимо потенцировать. После потенцирования нахожу искомые параметры регрессии:

b = b = 0.188

a = = = 7.831

Значит, степенное уравнение регрессии имеет вид . У степенной функции параметр b равен коэффициенту эластичности, поэтому можно сделать вывод, что при изменении среднего  времени простоя оборудования на 1% издержки на производство продукции в среднем изменятся на 0,188%.

Задание 3:

Для оценки тесноты связи в уравнении регрессии используют коэффициенты детерминации и корреляции.

Формулы для нахождения:

Коэффициента детерминации: R² = 1 -

Коэффициента корреляции: R =

3.1.Для  линейного уравнения регрессии:

R² = 1-  = 0.764 – вариация размера издержек на производство продукции на 76.4% объясняется вариацией среднего времени простоя оборудования; на долю прочих неучтенных факторов приходится 23.6%.

r = 0.874 – связь между размером издержек на производство продукции и средним временем простоя оборудования прямая тесная (неотрицательный, так как b является положительным).

3.2. Для степенного уравнения регрессии:

Для степенного уравнения регрессии нахождение коэффициентов детерминации и корреляции проводится по его линеаризованной форме: Ŷ=2.058+0.188⋅Х

R² = 1 -  = 0.690 – вариация размера издержек на производство продукции на 69% объясняется вариацией среднего времени простоя оборудования; на долю прочих неучтенных факторов приходится 31%.

R = 0.831 - связь между размером издержек на производство продукции и средним временем простоя оборудования тесная.

Задание 4:

Расчет средней ошибки аппроксимации необходим для определения качества модели. Найденную среднюю ошибку аппроксимации сравнивают с 8-10%. Если найденная ошибка меньше или равна 8-10%, то качество модели хорошее (или модель адекватна).