Microsoft Word. Microsoft Excel. MATLAB. Обработка матриц, страница 4

7.  Найти произведение  .

8.  Все элементы вектора  возвести с степень 2. В полученном векторе заменить первый элемент на номер вашего варианта.

9.  Получить диагональную матрицу, диагональные элементы которой будут равны вектору , а все остальные 0, найти сумму диагональных элементов.

.

Вариант 9

1.  Задать векторы, .

2.  Создать матрицу , у которой первая строка состоит из вектора , а вторая – из .

3.  Проверить существование обратной матрицы, если она существует – найти ее.

4.  Найти произведение . Из вектора  сделать новый, присоединив к нему элементы второго столбца матрицы .

5.  Найти вектор  и все элементы вектора  заменить значениями косинуса соответствующих элементов (, где - новое значение элемента вектора,  -начальное значение элемента) .

6.  С помощью созданной вами функции изменить матрицу следующим образом: каждый элемент квадратной матрицы   уменьшить на число, корое равняется размеру матрицы.

7.  Найти произведение .

8.  Найти вектор , который совпадает со вторым столбцом матрицы . В полученном векторе заменить первый элемент на номер вашего варианта.

9.  Получить среднее значение элементов вектора .

Вариант 10

1.  Определить матрицу .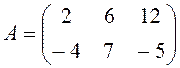

2.  Задать вектор .

3.  Проверить, существует ли обратная матрица для матрицы , которая получена в результате присоединения к матрице вектора  в качестве последней строки. Если существует, то найти ее.

4.   Получить вектор , который состоит из всех элементов матрицы , расположенных по убыванию.

5.  Найти произведение  .

6.  С помощью созданной вами функции найти вектор , где - произведение вектора-строки  на вектор-столбец .

7.  Найти произведение , предварительно оставив в векторе необходимое количество элементов.

8.  В полученном векторе заменить первый элемент на номер вашего варианта.

9.  Каждый элемент вектора  возвести в степень, которая совпадает с длиной вектора.

Вариант 11

1.  Определить матрицу .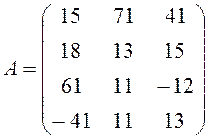

2.  Задать вектор .

3.  Из матрицы  сделать квадратную размера , в качестве последнего столбца взять вектор .

4.  Проверить существование обратной матрицы для . Если она существует, то найти ее.

5.  Найти произведение , а заменить вектор : каждый элемент умножить на определитель матрицы .

6.  С помощью созданной вам функции найти максимальный элемент матрицы   и затем умножить элементы второй строки на этот элемент.

7.  Найти произведение первой строки матрицы  на , получив вектор .

8.  В полученном векторе упорядочить элементы по возрастанию, а потом первый элемент заменить на номер вашего варианта.

9.  Получить матрицу, диагональные элементы которой будут составлять вектор , а все остальные - единицы.

Вариант 12

1.  Определить матрицу.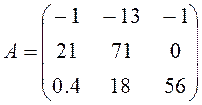

2.  Каждый элемент матрицы  разделить на определитель.  Резудьтат сохранить в переменной .

3.  Проверить существование обратной матрицы для . Если она существует, найти ее.

4.  Задать вектор , найти .

5.  Найти произведение элементов вектора .

6.  Создать функцию, с помощью которой можно определить максимальный элемент из двух векторов и создать матрицу , определитель которой будет равен этому элементу. Применить эту функция к векторам  и .

7.  Найти .

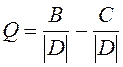8.  В полученном векторе заменить первый элемент на номер вашего варианта.

9.  Найти  , затем каждый элемент матрицы  возвести в степень 2.