8. В полученном векторе заменить первый элемент на номер вашего варианта.
9.
Каждый элемент вектора ![]() возвести в степень,
которая совпадает длиной вектора.
возвести в степень,
которая совпадает длиной вектора.
Вариант 4
1.
Определить матрицу 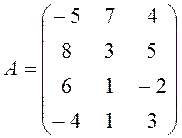 .
.
2.
Задать вектор ![]() .
.
3.
Из матрицы ![]() сделать квадратную
сделать квадратную ![]() , в качестве последнего столбца взять
вектор
, в качестве последнего столбца взять
вектор ![]() .
.
4. Проверить существование обратной матрицы, если она существует, то найти ее.
5.
Найти произведение ![]() , а потом заменить
вектор С: каждый элемент умножить на определитель матрицы
, а потом заменить
вектор С: каждый элемент умножить на определитель матрицы ![]() .
.
6.
С помощью созданной вами функции найти минимальный элемент матрицы ![]() и потом умножить элементы первой строки
матрицы
и потом умножить элементы первой строки
матрицы ![]() на этот элемент.
на этот элемент.
7.
Найти произведение первой строки матрицы ![]() на
на ![]() , получив вектор
, получив вектор ![]() .
.
8. В полученном векторе упорядочить элементы по убыванию, а потом первый элемент заменить на номер вашего варианта.
9.
Получить матрицу, диагональные элементы которой будут составлять вектор ![]() , а остальные – нули. Полученную матрицу
разделить на единичную.
, а остальные – нули. Полученную матрицу
разделить на единичную.
Вариант 5
1.
Определить матрицу 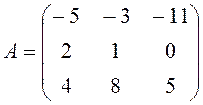 .
.
2.
Каждый элемент матрицы ![]() разделить на определитель.
Результат сохранить в переменной
разделить на определитель.
Результат сохранить в переменной ![]() .
.
3.
Проверить существование обратной матрицы ![]() . Если
существует – найти ее.
. Если
существует – найти ее.
4.
Задать вектор ![]() , найти
, найти ![]() .
.
5.
Найти максимальный элемент вектора ![]() .
.
6. Создать функцию с помощью которой можно определить модуль вектора.
7.
Найти 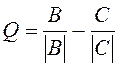 .
.
8. В полученном векторе заменить первый элемент на номер вашего варианта.
9.
Найти ![]() , а потом каждый элемент матрицы
, а потом каждый элемент матрицы ![]() возвести в степень 2.
возвести в степень 2.
Вариант 6
1.
Определить матрицу 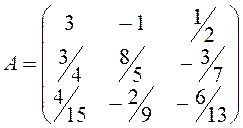 .
.
2.
Определить матрицу  .
.
3.
Найти матрицу ![]() такую, что
такую, что![]() .
.
4.
Найти обратную к ![]() матрицу.
матрицу.
5.
Найти произведение ![]() на
на ![]() .
.
6.
С помощью созданной вами функции найти матрицу ![]() ,
где
,
где ![]() - измененная матрица
- измененная матрица ![]() путем отбрасывания третьего столбца, а
путем отбрасывания третьего столбца, а ![]() - измененная путем отбрасывания третьей
строки.
- измененная путем отбрасывания третьей
строки.
7.
Матрицу ![]() изменить так, чтоб диагональные
элементы остались, а все остальные стали равны 0.
изменить так, чтоб диагональные
элементы остались, а все остальные стали равны 0.
8. В полученной матрице заменить первый элемент первой строки на номер вашего варианта.
9.
Определить максимальный элемент вектора, который является диагональю
матрицы ![]() .
.
Вариант 7
1.
Найти матрицу, транспонированную к 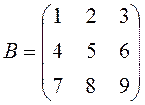 .
.
2.
Проверить существование обратной матрицы к ![]() . Если
да, то найти ее так, чтобы элементы обратной матрицы были представлены в виде
обыкновенных дробей.
. Если
да, то найти ее так, чтобы элементы обратной матрицы были представлены в виде
обыкновенных дробей.
3.
Задать матрицу ![]() , элементы которой заданы
следующим образом. 1-й столбец – вектор
, элементы которой заданы
следующим образом. 1-й столбец – вектор ![]() ; 2-й
столбец – это первый, упорядоченный по возрастанию, 3-й – это первый,
упорядоченный по убыванию.
; 2-й
столбец – это первый, упорядоченный по возрастанию, 3-й – это первый,
упорядоченный по убыванию.
4.
Найти ![]() и
и ![]() , которая
получена из матрицы
, которая
получена из матрицы![]() возведением каждого элемента в
степень 2.
возведением каждого элемента в
степень 2.
5.
Найти произведение первой строки матрицы ![]() на последний
столбец матрицы
на последний
столбец матрицы ![]() . Результат сохранить в
. Результат сохранить в ![]() .
.
6.
С помощью созданной вами функции найти вектор ![]() ,
который состоит из диагональных элементов матрицы
,
который состоит из диагональных элементов матрицы ![]() .
.
7.
Из матрицы ![]() сделать матрицу
сделать матрицу![]() с помою отбрасывания первой строки и
второго столбца.
с помою отбрасывания первой строки и
второго столбца.
8. В полученной матрице заменить первый элемент первой строки на номер вашего варианта.
9.
Найти вектор, состоящий из синусов соответствующих элементов вектора ![]() .
.
Вариант 8
1.
Определить матрицу ![]() размером
размером ![]() :
: 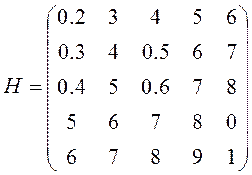 .
.
2. Проверить, существует ли обратная матрица, если да – найти ее.
3.
Задать вектор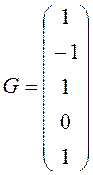 .
.
4.
Найти произведение ![]() .
.
5.
Найти вектор ![]() .
.
6.
С помощью созданных вами функций из матрицы ![]() сделать
матрицу размером
сделать
матрицу размером ![]() , оставив элементы левого нижнего
угла ( отбросив первые 2 строки и последние 2 столбца), а из вектора
, оставив элементы левого нижнего
угла ( отбросив первые 2 строки и последние 2 столбца), а из вектора ![]() сделать вектор размерности 3, отбросив
последние 2 элемента.
сделать вектор размерности 3, отбросив
последние 2 элемента.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.