Решение дифференциальных уравнений в пакете Simulink

Лабораторная работа № 2

Решение дифференциальных уравнений в пакете Simulink

Цель работы

1. Определение непрерывных моделей систем автоматического управления по заданным дифференциальным уравнениям или заданным передаточным функциям.

2. Определение матриц коэффициентов состояния, управления, наблюдения и выхода системы по дифференциальным уравнениям систем автоматического управления.

Теоретическое обоснование:

Классической формой представления однопараметрической математической модели системы является дифференциальное или операторное уравнение

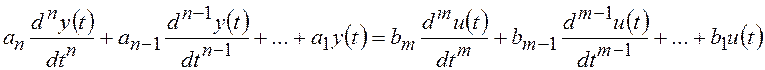, (3.1)

(a_nsⁿ + a_n-1s^n-1 +…+ a₁)×Y(s) = (b_ms^m + b_m-1s^m-1 +…+b₁)×U(s),                                                                                                               (3.2)

где u, у - входной и выходной сигналы системы управления, a_n, b_m – коэффициенты дифференциального или операторного уравнения.

Из выражения (3.2) определяется передаточная функция

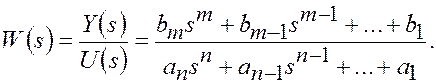                                    (3.3)

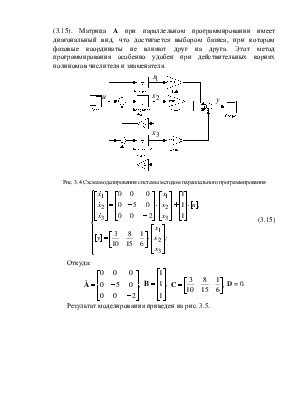
Одной передаточной функции системы управления (3.3) могут соответствовать несколько структурных схем, которые могут быть получены способами прямого, параллельного и последовательного программирования.

Непрерывная линейная система также может быть описана дифференциальным векторно-матричным уравнением

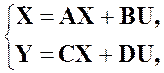                                                     (3.4)

где А – матрица коэффициентов состояний размером k´k; В – матрица коэффициентов управления размером k´n; С – матрица коэффициентов наблюдения размером m´k и D – матрица коэффициентов выхода размером m´n; X – вектор состояния (матрица-столбец размером k´1); U – вектор управления (матрица-столбец размером n´1); Y – вектор наблюдения (матрица-столбец размером m´1)[1]. Структурная схема вычисления значений векторно-матричных уравнений (3.4) изображена на рис. 3.1.

Описание работы

В пакете Simulink для передаточной функции (3.5) модели решения дифференциальных уравнений могут быть построены различными методами.

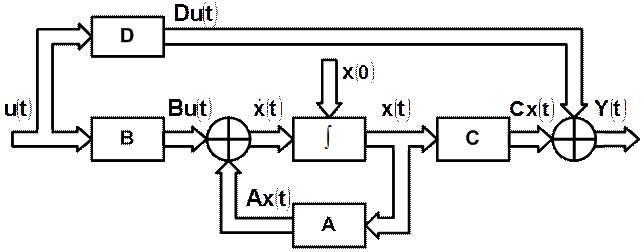
Рис. 3.1 Структурная схема вычисления значений векторно-матричных уравнений

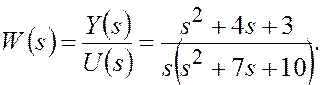                                   (3.5)

Метод прямого программирования

Изображение выходного сигнала можно определить через изображение дополнительной переменной e (3.6, 3.7).

Y(s) = (s² + 4s + 3)×E(s),                                       (3.6)

откуда

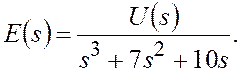                                       (3.7)

Уравнение (3.7) можно представить в виде дифференциального уравнения:

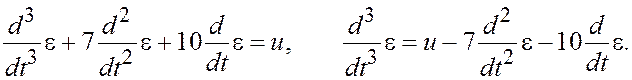               (3.8)

Уравнение (3.8) определяет схему моделирования (рис. 3.2). Выходная величина системы y(t) (3.6) является линейной комбинацией фазовых координат x_i. Фазовую координату интегратора 2 обозначают как x₁, то есть e = x₁, интегратора 1 – x₂, то есть 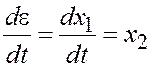, и так далее. Тогда фазовые координаты схемы моделирования рис. 3.2 связаны следующими соотношениями:

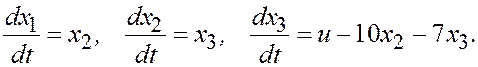                             (3.9)

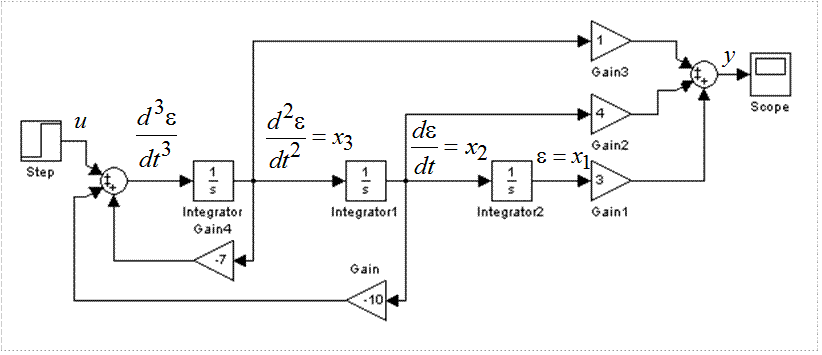
Рис.3.2 Схема моделирования системы методом прямого программирования

Выходная величина y(t) определяется как линейная комбинация фазовых координат (3.6)

y = 3x₁ + 4x₂ + x₃.                                                 (3.10)

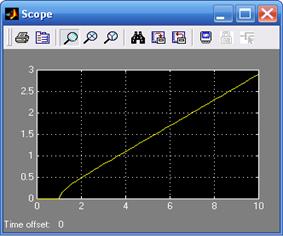
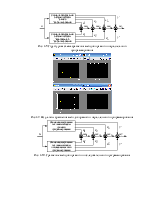
Рис. 3.3. Результат моделирования методом прямого программирования

Из системы уравнений (3.9) и 3.10) можно получить векторно-матричное уравнение системы и матрицы коэффициентов: состояний А, управления В и наблюдения С (3.11):

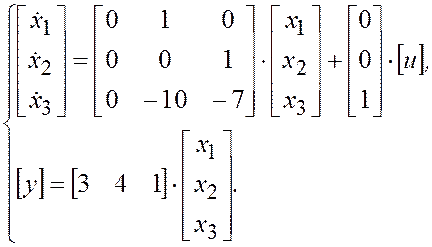                          (3.11)

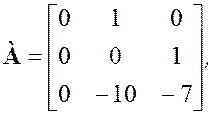
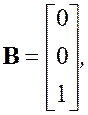  C = [3  4  1], D = 0;

Метод параллельного программирования

Структурная схема для параллельного программирования получается из передаточной функции (3.6), если ее представить в виде суммы элементарных дробей. Коэффициенты С₀, С₁, С₂, вычисленные методом Хевисайда, и корни знаменателя определяют с помощью программы:

coef=[1,7,10,0];                            %Коэффициенты многочлена

r=roots(coef)                               %Корни многочлена

syms s                                      %Символьнаяпеременная

C0=limit([(s^2+4*s+3)*s/(s^3+7*s^2+10*s)],0)     %Пределвточке s=0

Cl=limit([(s^2+4*s+3)*(s+5)/(s^3+7*s^2+10*s)],-5) %Пределвточке s=-5

C2=limit([(s^2+4*s+3)*(s+2)/(s^3+7*s^2+10*s)],-2) %Пределвточке s=-2

Откуда

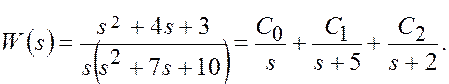                          (3.12)

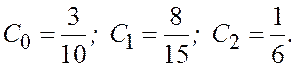                                                 (3.13)

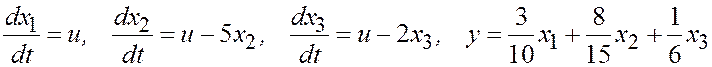.   (3.14)

С учетом выражений (3.13, 3.14) получена схема моделирования методом параллельного программирования (рис. 3.4).