Из каждой вершины тетраэдра SABC проведем отрезок, соединяющий эту вершину с центром масс (точкой пересечения медиан треугольника) противоположной грани. Обозначим эти отрезки АА’, ВВ’, СС’ и SS’. Они пересекаются в некоторой точке О.
Проекцией (гомоморфным отображением) тетраэдра SABC на плоскость (ABC) при центральном проектировании будет треугольник ABC. При этом проекциями отрезков АА’, ВВ’, СС’ будут соответственно медианы АА', ВВ', СС’ треугольника ABC, отрезок SS’ перейдет в точку S1 - точку пересечения вышеназванных медиан треугольника ABC.
Получили, что проекции пересекающихся в пространстве отрезков АА1 ВВ1, СС1 и SS1 пересекаются на плоскости в точке S1.
Естественно, напрашивается подобный вывод и при «проектировании» треугольника в тетраэдр, то есть перенос свойств объекта В на объект А. Такое заключение для данного случая имеет место, хотя в общем случае из условия пересечения проекций прямых на плоскости не следует их пересечение в пространстве.
Известно, что выводы по аналогии являются лишь гипотетическими суждениями, но в случае изоморфизма и гомоморфизма мы получаем достоверные заключения. Подлинный вывод по аналогии представляет собой гипотезу, которая не может быть логически обоснована, поэтому такие умозаключения необходимо в дальнейшем проверять. Однако наложение определенных дополнительных условий на выводы по аналогии может привести к ее частным достоверным случаям.
Другого подхода к трактовке строгой и нестрогой аналогии придерживаются авторы учебного пособия [8]. Аналогия может быть:
а) строгой аналогией, при которой признаки сравниваемых объектов находятся во взаимной зависимости;
б) нестрогой аналогией, при которой признаки сравниваемых объектов не находятся в явной взаимной зависимости.
Такое деление аналогии соответствует выделению двух типов моделирования. Первый вид - это моделирование однородное или физическое, когда модель обладает такими же физическими, химическими или иными чертами, как и сам образец, отличаясь от последнего лишь размерами. Второй вид - моделирование неоднородное, когда модель представлена совершенно в ином качестве, нежели образец, однако она подобна образцу в строго определенном интересующем исследователя отношении. Применительно к математике такое основание для деления может выразиться в рассмотрении аналогии между:
а) объектами, явно не относящимися к математике;
б) объектами, один из которых не относится к математике, а другой является математическим объектом;
в) объектами, являющимися математическими объектами. В свою очередь каждый из трех выделенных пунктов можно рассматривать отдельно и в каждом можно выделить различные виды аналогий.
Рассмотрим далее выделение некоторых видов аналогии в области геометрии. Для двух рассматриваемых геометрических объектов возможны три случая, а именно: или оба объекта являются планиметрическими, или оба стереометрическими, или один относится к планиметрии, а другой — к стереометрии. Поэтому в зависимости от принадлежности рассматриваемых объектов либо планиметрии, либо стереометрии можно выделить различные виды аналогий.
Аналогию между двумя объектами назовем внутренней, если аналогичные объекты изучаются либо в планиметрии, либо в стереометрии. Если один из объектов является планиметрическим, а другой - стереометрическим, то аналогию между ними назовем внешней. Таким образом, аналогия между прямоугольником и прямоугольным параллелепипедом, свойствами прямоугольника и сходными свойствами прямоугольного параллелепипеда будет внешней. А внутренней аналогией будет, например, аналогия между средней линией треугольника и средней линией трапеции, трехгранным углом и тетраэдром и так далее. Деление аналогии на внутреннюю и внешнюю не противоречит логике строения школьного курса геометрии - такое выделение двух видов аналогии согласуется с привычным делением геометрии на планиметрию и стереометрию.
Однако выделение геометрических фигур, отношений между ними, аксиом, теорем, задач характерно в равной степени как для планиметрии, так и для стереометрии. Поэтому в зависимости от рассматриваемых объектов выделим четыре вида аналогии в геометрии: аналогия между фигурами: аналогия между величинами; аналогия между отношениями; аналогия между задачами (теоремами, аксиомами). Обозначенные нами виды аналогии в геометрии можно для наглядности представить следующей схемой (рис. 2).
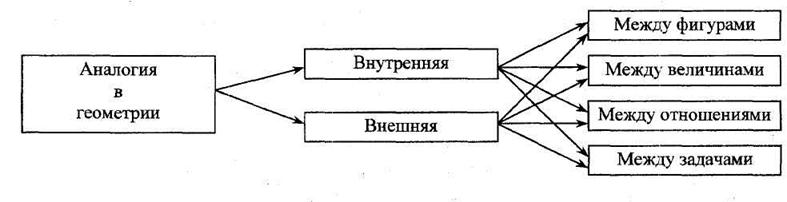
Рис. 2
В заключение отметим, что использование в обучении того или иного вида аналогии, как правило, подчиняется одной общей схеме, в которой можно выделить следующую последовательность этапов:
• принятие исходного объекта;
• выбор объекта, аналогичного исходному;
• сравнение исходного и аналогичного объектов;
• формулировка предположительного вывода по аналогии;
• доказательство или опровержение этого вывода;
• исследования по дальнейшему применению аналогии.
Однако цели использования аналогии, содержание учебного материала, уровень знаний учащихся, методические подходы учителя и другие причины несомненно будут накладывать свои коррективы на способы применения различных видов аналогии в обучении.
1. Сизова М.Н. Преемственность в формировании аналогии при обучении математике в начальных и 5-6 классах средней школы: Автореф. дисс.... канд. пед. наук. - Саранск, 1999. - 19 с.
2. Воробьев Н.В. Умозаключение по аналогии. - М.: Изд-во МГУ, 1963. - 26 с.
3. Ивин А.А. Искусство правильно мыслить: Книга для учащихся старших классов. - М.: Просвещение, 1986.-224 с.
4. Старченко А.А. Роль аналогии в познании. - М.: Высшая школа, 1961. - 52 с.
5. Уемов А.И. Аналогия в практике научного исследования. Из истории физико-математических наук. — М: Наука, 1970. - 264 с.
6. Уемов А.И. Логические основы метода моделирования. - М.: Мысль, 1971.-312 с.
7. Далингер В.А. Метод аналогии как средство обучения учащихся стереометрии: Учебное пособие. - Омск: Изд-во ОмГПУ, 1997. - 67 с.
8. Методика преподавания математики в средней школе. Общая методика. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов / В.А.Оганесян, Ю.М.Колягин, Г.Л.Луканкин, В.Я.Саннинский. - М.: Просвещение, 1980.-368 с.
9. Кондаков Н.И. Логика: Пособие для учителей. — М.: Учпедгиз, 1954. - 512 с.
10.Пойа Д. Как решать задачу. - М.: Учпедгиз, 1959. - 208 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.