Аналогия и ее виды в математике, страница 2

Сложение и умножение натуральных чисел обладают системой одинаковых свойств: коммутативность сложения (умножения); ассоциативность сложения (умножения); для натуральных чисел результат  операции  сложения  (умножения)  всегда  больше  любого слагаемого (множителя); результат сложения (умножения) двух не равных нулю чисел всегда можно проверить с помощью обратной операции вычитания (деления) и другие.

Сходство в свойствах чисел, делящихся на 3 или на 9, дает возможность говорить об атрибутивной аналогии между признаками делимости чисел на 3 и на 9. Сравним: для делимости на 3 нужно, чтобы сумма цифр числа делилась на 3; для делимости на 9 нужно, чтобы сумма цифр числа делилась на 9.

Приведем пример релятивной аналогии.

Прямая в прямоугольной системе координат, проходящая через точку (0; 0), задается уравнением у=кх. Между координатами точек этой прямой можно установить релятивную аналогию. Действительно, из уравнения у=кх получаем, что 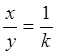 а значит, абсцисса точки относится к ее ординате, как 1 относится к к. Тогда упорядоченная пара чисел, первое из которых в к раз меньше второго, аналогична любой другой паре упорядоченных чисел, также удовлетворяющих описываемому отношению. А это значит, что координаты произвольной точки прямой у=кх аналогичны координатам любой другой точки этой прямой.

Заметим, что данный пример характеризуется пропорцией 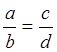Тогда между парой чисел а - b и парой с - d существует аналогия, основанная на равенстве отношений между этими числами. Н.В. Воробьев говорит о таком виде аналогии, как о частном случае аналогии отношений. Например, «система двух чисел 6 и 9 аналогична системе чисел 10 и 15, поскольку можно составить следующую пропорцию 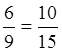» [2. С. 16].

Если в основу положить виды тождеств, существующих в математике, и найти им аналогию, то возможно выделить шесть ее основных видов в математике: аналогия применения, аналогия обобщения, аналогия контакта, предельная аналогия, аналогия преобразований, тривиальная аналогия. Характеристики этих видов аналогии и соответствующие примеры приведены в учебном пособии [7]. Однако аналогию подобного рода можно установить и между объектами, не являющимися тождественными с точки зрения математики. Поэтому мы считаем, что приведенные выше шесть типов аналогии целесообразно дополнить еще одним типом - аналогией противоположностей.

Если в рассматриваемой паре объектов установление какого-либо свойства одного объекта дает возможность говорить о противоположном (взаимообратном) свойстве другого объекта, то можно говорить об аналогии между этими объектами - аналогии противоположностей.

Например, такая аналогия существует между процессами нагревания и охлаждения. Так, соответственно, увеличивается или уменьшается скорость движения атомов, расширяются или сжимаются физические тела, повышается или понижается давление жидкости в закрытом сосуде, увеличивается или уменьшается сопротивление проводника электрического тока и др. Практически всегда противопоставляемые объекты обладают и одинаковой системой свойств. Так, либо сильно нагретые, либо сильно охлажденные тела вызывают одинаковую реакцию человеческого организма - ожог. Тепло, так же как и холод, фокусируется, передается при контакте от одного тела к другому.

В математике объекты, между которыми можно установить аналогию противоположностей, довольно часто рассматривают совместно. При этом выделяют как общие свойства объектов, так и противоположные. Например, аналогию противоположностей можно установить между взаимообратными функциями f(х)=ln x и g(x)=e^x.

Для функций f(x)= log_aX и g(x)=a^x характерна общность в свойствах, связанных с изменением параметра а. Наиболее часто говорят об интервалах монотонности: если 0<а<1, то функции f(x) и g(x) убывают на всей области определения, если а>1, то функции f(x) и g{x) возрастают на всей области определения.

Таким образом, возможно выделить семь видов аналогии, и такая типология будет основываться на видах тождеств, существующих в математике.

Помимо приведенных типологизаций аналогии, существуют и другие способы ее деления на виды. Покажем наиболее распространенные. Одну из них можно наглядно охарактеризовать следующей схемой (рис. 1).

Рис. 1

Тогда, в зависимости от направления вывода, можно выделить два вида аналогии. В литературе [8, 9] такие виды аналогии называют простой и распространенной аналогией.

Простая аналогия характеризуется тем, что по сходству объектов в некоторых признаках заключают об их сходстве в других признаках. Распространенная аналогия характеризуется тем, что из сходства явлений делают вывод о сходстве причин.

Представляет интерес выделение еще двух видов аналогии, которая может быть «строгой» и «нестрогой». Однако под одинаковыми названиями у разных авторов нередко подразумевается различный смысл.

Иногда выделение видов аналогии основано на логической ценности знания, полученного с ее помощью, и тогда деление ставится в прямую связь с условиями правомерности вывода по аналогии [4]. В этом случае рассмотрение строгой и нестрогой аналогии будет соответствовать изучению дедуктивной и индуктивной аналогии.

Как частный случай дедуктивной аналогии выделим понятие изоморфизма Изоморфизм есть строго фиксируемое отношение сопоставляемых объектов, между которыми существует взаимно однозначное соответствие элементов, связей и свойств. В силу свойства симметричности изоморфизма свойства, установленные для любого из исследуемых объектов, могут быть перенесены на другой, изоморфный ему объект. Д. Пойа говорит об изоморфизме как о случае, в котором аналогия достигает точности математического понятия [10. С. 51].

Например, взаимно однозначное соответствие между множеством пар действительных чисел и множеством радиус-векторов в прямоугольной системе координат позволяет исследовать свойства операции сложения радиус-векторов посредством исследования аналогичной операции на множестве пар действительных чисел.

Наряду с понятием изоморфизма, встречается понятие гомоморфизма, которое считается более общим, чём изоморфизм, поскольку гомоморфизм не требует взаимно однозначного соответствия элементов сравниваемых систем. Поэтому при исследовании объекта А и гомоморфного ему объекта В свойства объекта А с достоверностью можно переносить на объект В, однако нельзя утверждать, что свойства, установленные для объекта В, будут выполняться и для объекта Л (хотя это возможно).

Рассмотрим пример, в котором объектом А будет являться тетраэдр, объектом В - треугольник, а центральное проектирование пространственных тел на плоскость -гомоморфным отображением.