Разбивка полигона на местности. Камеральная обработка ведомости координат. Построение плана полигона, страница 2

Σβ_теор. = 180^о·(n – 2),                                                                      (2)

где n – число углов полигона и определяют угловую невязку по формуле

f_β = Σβ_изм. - Σβ_теор.                                                                           (3)

Если невязка в углах не превышает допустимой величины, вычисляемой по формуле

f_{β доп.}= ±1΄√n ,                                                                             (4)

то ее распределяют с обратным знаков поровну (с округлением значений поправок до 1΄) на углы, заключенные между короткими  сторонами полигона. Попрвки с их знаками выписывают над значениями соответствующих измеренных углов. Сумма поправок должна равняться невязке с обратным знаком.

в) Учитывая поправки, вычисляют исправленные углы. Их сумма должна быть точно равна теоретической сумме углов

Σβ_изм. = Σβ_теор.   

 2.  Вычисление азимутов и румбов.

а)  По исходному азимуту (дирекционному углу) А_1-2 (α_1-2) соответствующего варианта и исправленным углам вычисляют азимуты (дирекционные углы) всех других сторон по формуле

α_посл. = α_пред.  +180^о – β_прав.                                                        (5)        

Если в процессе вычислений азимут (дирекционный угол) какой-либо стороны окажет больше 360^о, то от него необходимо отнять 360^о.

В результате последовательного вычисления азимутов (дирекционных углов) сторон замкнутого полигона должен получиться азимут (дирекционный угол) начальной стороны полигона (α_1-2 ).  б) Азимуты переводят в румбы по формулам:

Направление	А, град	r
СВ	0...90	А
ЮВ	90...180	180°-A
ЮЗ	180...270	A-180о
СЗ	270...360	360° -А

3. Вычисление приращений координат.

а) По горизонтальным проложениям линий (S) и румбам (r) вычисляют приращения координат ΔX и ΔY по формулам

ΔX = S· cos r

ΔY = S· sin r .                                                                     (6)

б) Результаты вычислений записывают в ведомость координат с округлением до 0,01 м.

в) Знаки приращений координат зависят от названия румбов:

Название румбов	Х	Y
СВ ЮВ ЮЗ СЗ	+ - - +	+ + - -

4. Определение линейной невязки в полигоне и увязка приращений.

а) Вычисляют невязки в приращениях по осям X и Y по формулам

f_x = ΣΔX_практ. - ΣΔX_теор.               

f_y = ΣΔY_практ. - ΣΔY_теор.                                                        (7)

Для замкнутого полигона теоретические суммы    ΣΔX_теор. и  ΣΔY_теор. равны нулю.   б) Вычисляют абсолютную невязку  f_абс. в полигоне по формуле

 ,                                                              (8)     

а затем относительную невязку в периметре по формуле

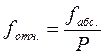 ,                                                                         (9)    

где Р периметр полигона.

в) Если относительная невязка в периметре окажется меньше допустимой           (f_доп. =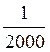), то невязки ΔX и ΔY распределяют с обратным знаком на все приращения координат пропорционально длинам линий.

Поправки выписывают над соответствующими приращениями.

Сумма поправок в приращениях по каждой оси должна равняться невязке с обратным знаком.

г) С учетом поправок вычисляют исправленные приращения координат.

Алгебраические суммы исправленных приращений координат должны быть равны нулю (ΣΔX_испр..=0; ΣΔY_испр.=0).

5. Вычисление координат вершин полигона.

На основании координат вершины 1 полигона и исправленных приращений координат вычисляют координаты остальных вершин по формулам

X_{послед.}= X_пред. + ΔX_испр.

Y_{послед.} = Y_пред. + ΔY_испр.                                                      (10)

В результате последовательного вычисления координат всех вершин замкнутого полигона должны получиться координаты вершины 1 (контроль).

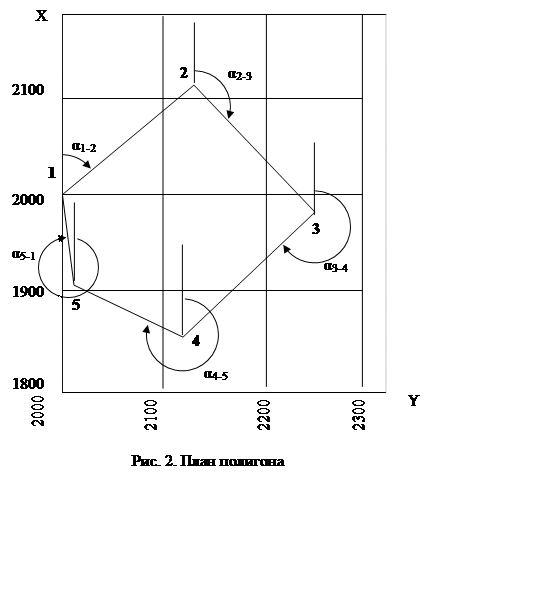
6. Составление плана полигона по координатам его вершин.

а) На бумагу наносят вершину 1 полигона с таким расчетом, чтобы полигон разместился симметрично относительно краев листа бумаги.

б) Строят координатную сетку со стороной квадрата 10 см при помощи масштабной линейки и измерителя по способу засечек, известному их геометрии. Для чего через намеченную точку 1 (с координатами X= +2000 и Y= +2000) проводят ось ординат, а перпендикулярно к ней ось абсцисс (рис. 2).

в) Все вершины полигона последовательно наносят на бумагу по координатам с помощью масштабной линейки и измерителя. Измеренные на плане длины линий должны быть равны горизонтальным проложениям длин соответствующих линий в ведомости (контроль). Расхождения не должны превышать 0,2 мм. Измеренные транспортиром азимуты (дирекционные углы) должны быть равны соответствующим углам ведомости координат.

 

Исходные данные

Исходные данные указаны в ведомости координат (табл. 1). Для различных вариантов дирекционный угол  линии 1-2 будет  следующим:

α_1-2 = 51^о06΄ + №_вар^о №_вар΄.