Определение показателей сопротивляемости грунтов сдвигу. Методы определения

Лекция № 6

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ СОПРОТИВЛЯЕМОСТИ

ГРУНТОВ СДВИГУ

МЕТОДЫ ОПРЕДЕЛЕНИЯ

Определение показателей сопротивляемости сдвигу сыпучих

(несвязных) грунтов

1. В  трехосном напряженном состоянии.

Сопротивляемость сдвигу сыпучих грунтов, в особенности с крупными включениями, наиболее полно и разносторонне изучена в трехосном напряженном состоянии. Для этой цели созданы специальные аппараты — стабилометры. Принципиальная схема стабилометра приведена на рис. 2.

Сущность испытания грунтов в стабилометре заключается в следующем. Образец грунта, имеющий форму цилиндра с высотой, превышающей его диаметр в 2—3 раза, заключают в резиновую рубашку. Далее образец помещают в цилиндр стабилометра, прибор герметически закрывают и к образцу прилагают   вертикальную   нагрузку напряжением   р₁ и   с   одновременным всесторонним обжатием с боков напряжением р₂. Вертикальное давление р₁ создает приложенная к поршню прибора сила Р = р₁·F, где F— площадь сечения образца. Боковое давление на образец передает жидкость (вода, глицерин), нагнетаемая в цилиндр стабилометра под тем или иным давлением  р₂ специальным насосом. Конечная цель опыта заключается в  установлении  величины вертикального  сжимающего  напряжения р₁, при котором в условиях скола разрушается образец  при  некоторой  величине всестороннего бокового обжатия р₂. Опыты проводятся в различных вариантах:   а) при постоянной величине бокового давления р₂  и постепенном    увеличении  сжимающего напряжения р₁  вплоть до разрушения образца; б) при постоянной величине вертикального давления и постепенном ослаблении бокового давления р₂ также до разрушения образца.

По полученным критическим значениям p_1кp и р_2кр, отвечающим разрушению образца определяют величины угла внутреннего трения φ_n и зацепления с_n с пoследующим расчетом s_рn по формуле:

s_рn = p·tgφ_n + с_n                                                  (7)  

1. Для случая предельно рыхлого состояния сыпучего грунта, когда зацепление в нем отсутствует и выражение (7) упрощается:

s_рn = p·tgφ_n                                                       (8)

Следует иметь в виду, что сопротивляемость s_pn грунта  сдвигу  соответствует предельному сопротивлению его сдвигу при зафиксированном разрушении или течении  образца породы: s_pn = τ_кр.

	Рис.   Рис. 3.   Круги   напряжений для рыхлого  сыпучего  грунта   (с = 0): круги А и  В отвечают грунту в состоянии предельного равновесия;  круг В — то же,  в допредельном состоянии

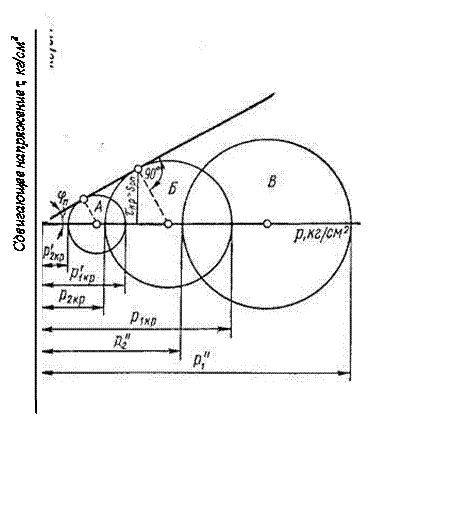
Предельная кривая, огибающая круги напряжений, построенные на p_1кp и p_2кp при соблюдении указанного выше условия, будет представлять собой прямую в координатных осях s_pn= f(p), соответствующую уравнению (8). Эта линия будет иметь угловой коэффициент tgφ и проходить через начало координат. При этом условии прямая в рассматриваемом случае предельного равновесия будет отходить от оси абсцисс под углом, равным углу внутреннего трения  грунта  φ_n.

2. Для общего случая, соответствующего зависимости (7)

s_рn = p·tgφ_n + с_n  , для практического использования которой необходимо знать угол внутреннего трения φ_n и зацепление с_n.

Величины этих двух показателей определяют экспериментально последовательным проведением двух опытов на двух образцах породы с одинаковой заданной плотностью (по пористости) при различных исходных значениях бокового давления p_2кp и вертикальных нагрузок p_1кp. В этом случае (рис.4 )  касательная составит с горизонтальной осью координат угол, равный  углу внутреннего трения φ_n, и вместе с тем отсечет на оси ординат отрезок (свободный член линейного уравнения).  Продолжение касательной влево, вплоть до пересечения с осью абсцисс, даст на этой оси отрезок