Дисциплина: ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ
Раздел: МАСШТАБЫ ПЛАНОВ И КАРТ
Цель работы: научиться пользоваться стандартными масштабами, строить номограммы линейного и поперечного масштабов и применять их в геодезической практике, производить по карте измерение длин линий..
Необходимые материалы и принадлежности: учебная карта У-42-73-В, учебная карта У-41-144-Б, фрагменты карт комплекта №7-100, циркуль-измеритель, линейка, карандаш.
Тема: ЧИСЛЕННЫЙ И ЛИНЕЙНЫЙ МАСШТАБ
Основные положения
Используя значение 1/М числового масштаба и зная длину S проложения линии на местности, можно по формуле
s=S/М (1.1)
определить ее длину на плане
или по формуле
S=sМ (1.2)
определить длину линии на местности, зная длину s этого отрезка на плане.
Пример 1. Длина отрезка S= 142 м. Найти величину изображения этого отрезка на плане масштаба 1:2000.
По формуле (1.1) получим s = 142 м/2000 = 0,071 м = 7,1 см.
Пример 2. На плане масштаба 1:500 величина отрезка между двумя точками s=14,6 см. Определить длину S этой линии на местности.
По формуле (1.2) находим S=14,6 см x 500=7300 см =73 м.
ЗАДАНИЕ №1
Дано расстояние между двумя точками на карте l. Определить длину горизонтального проложения соответствующей линии местности S, если масштаб карты 1 : М равен: 1) 1 : 2000; 2) 1 : 5000; 3) 1 : 10 000; 4) 1 : 25 000 (табл. 1).
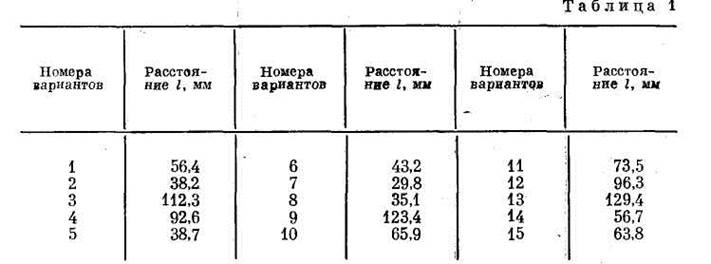
Решение. Вычисление производится по формуле
S = lM,
где М — знаменатель численного масштаба, показывающий, во сколько раз линии местности уменьшены при их изображении на карте.
Например, если 1 : М = 1 : 2000 и l = 56,4 мм, то d =56,4 мм ×2000 = 112 800 мм = 112,8 м.
ЗАДАНИЕ №2
|
|
Дано горизонтальное проложение dлиний местности. Определить с точностью 0,1 мм длину соответствующих линий на картах следующих масштабов: 1) 1 : 2000; 2) 1 : 5000; 3) 1 : 10 000 (табл. 2).
![]() Решение. Вычисления выполняют по формуле
Решение. Вычисления выполняют по формуле
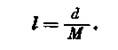
Если, например, d= 78,0 м = 78 000 мм, то I= 78 000 : 2000 = = 39,0 мм на карте масштаба 1 : 2000.
Тема: ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ НА ТОПОГРАФИЧЕСКОЙ КАРТЕ
С ПОМОЩЬЮ ЛИНЕЙНОГО И ПОПЕРЕЧНОГО МАСШТАБОВ
Рассмотрим пример построения линейного масштаба и пользования им, если численный масштаб равен 1 : 5000. Приняв за основание отрезок в 1 см, соответствующий 50 м на местности, откладывают его несколько раз по прямой и подписывают, как указано на рис. 1, а. Левое основание делят на пять или десять частей. Теперь, взяв расстояние на плане в раствор циркуля-измерителя, одну его ножку устанавливают на штрих, разделяющий основания, но так, чтобы другая ножка попала слева от 0 до 50.
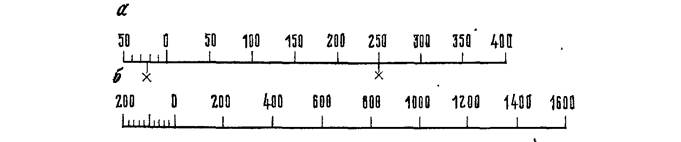
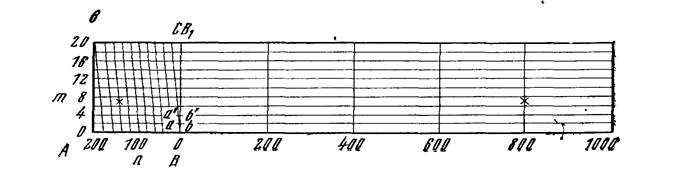
Рис. 1. Номограммы масштабов
Построение линейного масштаба, когда знаменатель численного масштаба не выражается круглым числом, что бывает при пользовании аэрофотоснимком местности, по существу ничем не отличается от только что сказанного. Например, масштаб аэрофотоснимка 1 : 17 380. Согласно условиям, указанным выше, основание линейного масштаба должно соответствовать 200 м, а длина его определится из соотношения
1 см соответствует 173,8 м, х см - 200,0 м, следовательно,
![]()
Величину этого отрезка несколько раз откладывают на прямой, левое основание делят на части и масштаб вычерчивают, как показано на рис. 1, б.
Так как доли деления по линейному масштабу оценивают на глаз, что снижает точность измерения расстояний, то пользуются поперечным масштабом (рис. 8, в), который строят следующим образом. Выбирают основание масштаба АВ (см. рис. 8, в), как и линейного, и откладывают его несколько раз на прямой. Из полученных точек восставляют перпендикуляры к этой прямой (или проводят параллельные линии, не перпендикулярные к прямой). Левое основание делят на 5 или 10 равных делений, в общем случае на п делений, а на перпендикулярах откладывают т равных делений (тоже 5 или 10) произвольной длины, но в целом не более 3 см. Через полученные точки на перпендикулярах проводят линии, параллельные основанию.
Затем на левом основании через все деления проводят линии, параллельные ВС, как показано на рис. 8, в, называемые трансверсалями. Отрезок ab называется наименьшим делением поперечного масштаба. Величина его зависит от длины основания АВ и числа делений п . Из подобия треугольников ВСВ1 и Ваb следует, что
![]()
откуда
![]()
![]()
поэтому
![]()
т. е. наименьшее деление поперечного масштаба равно основанию, деленному на произведение чисел п и т.
Для масштаба 1 : 10 000, изображенного на рис. 1, в, основание АВ, равное 2 см, соответствует 200 м на местности. Число делений п = 10 и m = 10, поэтому наименьшее деление поперечного масштаба соответствует ab =200/(10х10) = 2 м на местности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.