Исследование типовых динамических звеньев, страница 3

Рис.1.12. Переходные функции                                         Рис. 1.13. Весовые функции

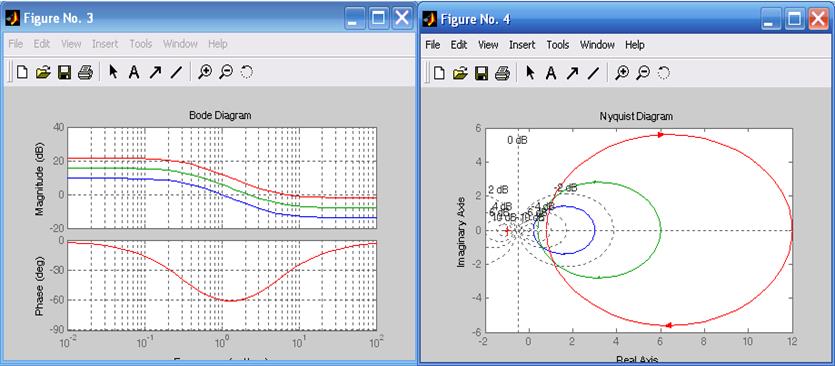
Рис. 1.14. АЧХ и ФЧХ                                   Рис. 1.15. Амплитудно-фазовые характеристики

Определение характеристик инерционно-форсирующего звена в зависимости от постоянной времени представлены на рис. 1.16 – 1.19:

h1=tf(k*[T0,1],[T,1]);            %Передаточная функция при T=3

h2=tf(k*[T0,1],[2*T,1]);          %Передаточная функция при T=6

h3=tf(k*[T0,1],[4*T,1]);          %Передаточная функция при T=12

figure(1),step(h1,h2,h3),grid          %Переходныефункции

figure(2),impulse(h1,h2,h3),grid       %Весовыефункции

figure(3),bode(h1,h2,h3),grid          %АЧХиФЧХ

figure(4),nyquist(h1,h2,h3),grid       %АФХ

symss                                 %Ввод символьных переменных

hp1=ilaplace(k*(T0*s+1)/(s*(T*s+1)))   %Обратное преобразование

hp2=ilaplace(k*(T0*s+1)/(s*(2*T*s+1))) %Лапласаизображений

hp3=ilaplace(k*(T0*s+1)/(s*(4*T*s+1))) %переходныхфункций

hi1=ilaplace(k*(T0*s+1)/(T*s+1))       %Обратное преобразование

hi2=ilaplace(k*(T0*s+1)/(2*T*s+1))     %Лапласа изображений

hi3=ilaplace(k*(T0*s+1)/(4*T*s+1))     %весовых функций

ltiview(h1,h2,h3)                      %Просмотр характеристик

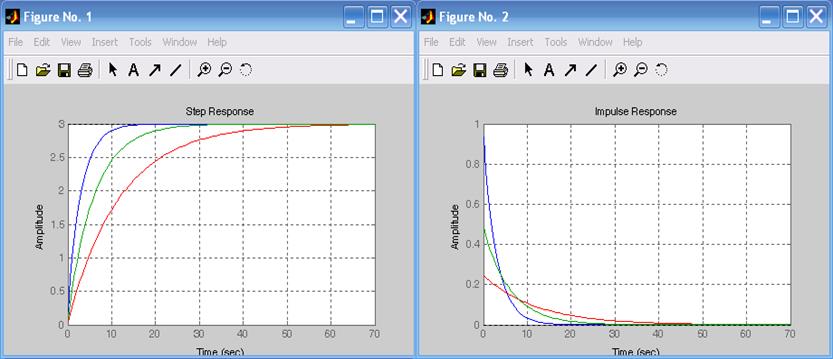
Рис.1.16. Переходные функции                                      Рис. 1.17. Весовые функции

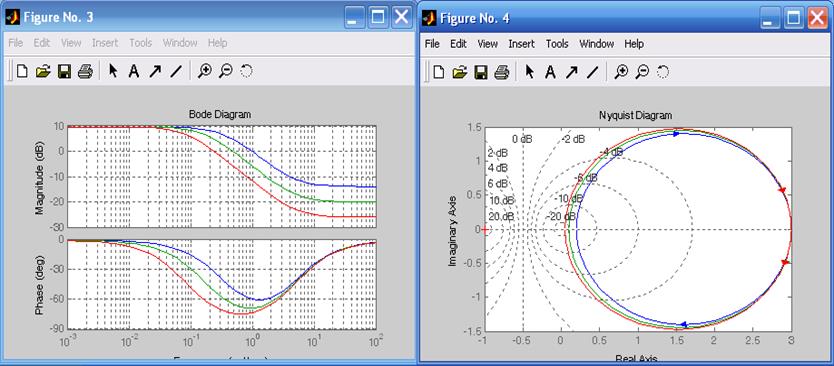
Рис. 1.18. АЧХ и ФЧХ                       Рис. 1.19. Амплитудно-фазовые характеристики

Определение временных и частотных характеристик колебательного звена 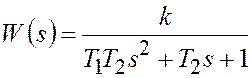 в зависимости от коэффициента усиления k:

k=3;                              %Коэффициент усиления

T1=0.1;                           %Постоянная времени Т1

T2=0.2;                           %Постоянная времени Т2

h1=tf(k,[T1*T2,T2,1]);            %Передаточная функция при k=3

h2=tf(2*k,[T1*T2,T2,1]);          %Передаточная функция при k=6

h3=tf(4*k,[T1*T2,T2,1]);          %Передаточная функция при k=12

figure(1),step(h1,h2,h3),grid     %Переходныефункции

figure(2),impulse(h1,h2,h3),grid  %Весовыефункции

figure(3),bode(h1,h2,h3),grid     %АЧХиФЧХ

figure(4),nyquist(h1,h2,h3),grid  %Амплитудно-фазовыехарактеристики

symss                                 %Ввод символьных переменных

hp1=ilaplace(k/(s*(T1*T2*s^2+T2*s+1))  %Обратное преобразование

hp2=ilaplace(k/(s*(2*T1*T2*s^2+T2*s+1)) %Лапласаизображений

hp3=ilaplace(k/(s*(4*T1*T2*s^2+T2*s+1)) %переходныхфункций

hi1=ilaplace(k/(T1*T2*s^2+T2*s+1))     %Обратное преобразование

hi2=ilaplace(k/(2*T1*T2*s^2+T2*s+1))   %Лапласа изображений

hi3=ilaplace(k/(4*T1*T2*s^2+T2*s+1))   %весовых функций

ltiview(h1,h2,h3)                      %Просмотр характеристик

Результаты исследования представлены на рис. 1.20 – 1.23.

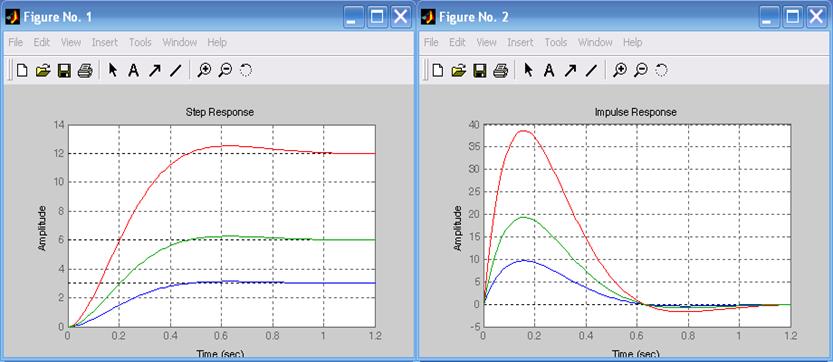
Рис.1.20. Переходные функции                                         Рис. 1.21. Весовые функции

Определение временных и частотных характеристик колебательного звена 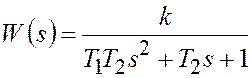 в зависимости от постоянной времени T₁:

k=3;T1=0.1;T2=0.2;  %Коэффициент усиления, постоянные времени Т1,Т2

h1=tf(k,[T1*T2,T2,1]);            %Передаточная функция при T1=0.1

h2=tf(k,[2*T1*T2,T2,1]);          %Передаточная функция при T1=0.2

h3=tf(k,[4*T1*T2,T2,1]);          %Передаточная функция при T1=0.4

figure(1),step(h1,h2,h3),grid     %Переходныефункции

figure(2),impulse(h1,h2,h3),grid  %Весовыефункции

figure(3),bode(h1,h2,h3),grid          %АЧХиФЧХ

figure(4),nyquist(h1,h2,h3),grid       %АФХ

symss                                 %Ввод символьных переменных

hp1=ilaplace(k/(s*(T1*T2*s^2+T2*s+1))  %Обратное преобразование

hp2=ilaplace(k/(s*(2*T1*T2*s^2+T2*s+1)) %Лапласаизображений

hp3=ilaplace(k/(s*(4*T1*T2*s^2+T2*s+1)) %переходныхфункций