Наблюдаемые и операторы. Операторы квантовой механики. Соотношения неопределённости

Лекция №3.

План лекции:

наблюдаемые и операторы,

операторы квантовой механики,

соотношения неопределённости.

Ключевые слова:

среднее значение наблюдаемой

оператор импульса оператор момента оператор Гамильтона

соотношения неопределённости для координаты и импульса

Наблюдаемые и операторы.

Теперь необходимо установить соответствие между рассмотренным выше математическим аппаратом и физическим содержанием теории. Это соответствие устанавливается с помощью ряда утверждений, которые наряду с понятием волновой функции и принципом суперпозиции составляют основу квантовой механики. Перейдём к формулировке этих утверждений.

Каждой динамической переменной (наблюдаемой) в квантовой механике ставится в соответствие линейный, самосопряжённый оператор.

Указанное соответствие подразумевает, что соотношения между динамическими переменными, которые имеют место в классической механике, справедливы в квантовой механике для операторов этих переменных.

Спектр собственных значений наблюдаемой совпадает со спектром собственных значений оператора, соответствующего этой наблюдаемой.

Таким образом, для того чтобы предсказать значения наблюдаемой, которые могут быть получены в результате её измерения, достаточно найти спектр собственных значений соответствующего оператора.

Следующее утверждение определяет процедуру нахождения среднего значения наблюдаемой. Выражение, которое определяет среднее значение, является обобщением формулы (1.11). Пусть q - совокупность координат системы, а dq – произведение дифференциалов этих координат (элемент конфигурационного пространства).

Среднее значение наблюдаемой для системы, находящейся в состоянии, которое описывается волновой функцией  определяется выражением

                                        (1.30),

где интегрирование проводится по всему конфигурационному пространству.

В частности для одной частицы, местоположение которой задаётся радиус-вектором , формула приобретает вид

                                        (1.31).

Проведём разложение подынтегральной волновой функции по полному набору собственных функций оператора (ограничимся для простоты одномерным случаем, и будем считать, что оператор обладает дискретным спектром собственных значений ). Тогда с учётом условия ортонормированности (1.21) получим

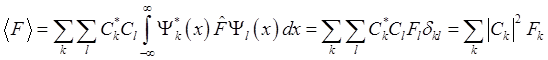      (1.32), где коэффициенты  удовлетворяют условию полноты набора (1.23). Из последнего выражения следует, что квадрат модуля коэффициента  равен вероятности получения k-ого собственного значения наблюдаемой F.  Условие полноты набора при этом отражает то обстоятельство, что вероятность получения при измерении одного из собственных значений равна единице.

В состояниях, которые описываются собственными функциями оператора , среднее значение совпадает с собственным значением оператора. Действительно, подставляя в формулу (1.31) правую часть равенства , с учётом условия нормировки (1.1) получим . Рассмотренные состояния, помимо только что доказанного свойства, обладают ещё одной важной особенностью. В этих состояниях дисперсия , которая характеризует разброс значений наблюдаемой F равна 0, в чём нетрудно убедиться непосредственным вычислением. Имеет место и обратное свойство - состояния, в которых дисперсия  F равна нулю, описываются собственными функциями оператора . Для доказательства введём самосопряжённый оператор . С помощью этого оператора выражение для дисперсии можно представить в виде

Действительно, подставляя явный вид оператора , получим обычное выражение для дисперсии:

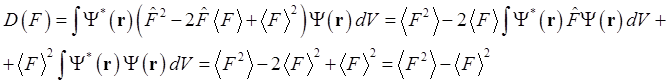
Итак, пусть . Тогда, применяя условие эрмитовости оператора (1.14) к оператору , получим

.

Как видно из полученной формулы, стоящее под знаком интеграла выражение неотрицательно. Это означает, что интеграл может быть равен нулю лишь при условии , откуда следует, что , где . Из полученных результатов следует, что в состоянии, которое описывается собственной функцией оператора , наблюдаемая F имеет определённое значение, равное соответствующему собственному значению оператора.  В произвольном состоянии с некоторой вероятностью может быть получено любое из собственных значений наблюдаемой.

Операторы квантовой механики.