Установим теперь явный вид
операторов квантовой механики. Ранее было показано, что оператор координаты
сводится к умножению на координату ![]() . Для того,
чтобы найти вид остальных операторов, помимо оператора координаты нужно задать
ещё оператор импульса.
. Для того,
чтобы найти вид остальных операторов, помимо оператора координаты нужно задать
ещё оператор импульса.
В квантовой механике вектору импульса ставится в соответствие дифференциальный векторный оператор вида
![]() (1.33).
(1.33).
Хотя данное определение носит аксиоматический характер в его пользу можно высказать ряд соображений, некоторые из которых будут рассмотрены ниже.
Найдём собственные
функции и спектр собственных значений оператора ![]() .
Уравнение для собственных функций проекции оператора
.
Уравнение для собственных функций проекции оператора ![]() имеет вид
имеет вид
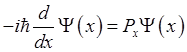 (1.34)
(1.34)
Его решением является волновая функция вида
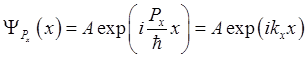 (1.35), где введено обозначение
(1.35), где введено обозначение ![]() .
Функция удовлетворяет стандартным требованиям при любых
.
Функция удовлетворяет стандартным требованиям при любых ![]() , спектр значений которых, таким образом,
является непрерывным. Коэффициент A
определится из условия нормировки (1.25), которое в данном
конкретном случае имеет вид
, спектр значений которых, таким образом,
является непрерывным. Коэффициент A
определится из условия нормировки (1.25), которое в данном
конкретном случае имеет вид
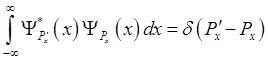 (1.36).
(1.36).
Отсюда, используя интегральное представление ![]() -функции
-функции
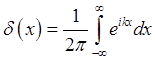 (1.37), а также её свойство
(1.37), а также её свойство
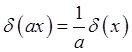 (1.38)
(1.38)
получим ![]() . Собственную
функцию оператора
. Собственную
функцию оператора ![]() можно представить, как
произведение собственных функций его проекций
можно представить, как
произведение собственных функций его проекций
![]() (1.39), где
(1.39), где ![]() .
.
После того как были определены операторы
координаты и импульса, можно найти явный вид других операторов квантовой
механики. В частности оператор
момента ![]() определяется как
векторное произведение операторов координаты и импульса
определяется как
векторное произведение операторов координаты и импульса
![]() (1.40).
(1.40).
Оператор
Гамильтона представляет собой сумму операторов кинетической и
потенциальной энергии. В частности для одной частицы в потенциальном поле ![]() имеем
имеем
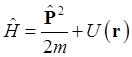 (1.41).
(1.41).
Соотношения неопределённости.
Выше было установлено, что условием существования определённого значения наблюдаемой в некотором состоянии является требование, чтобы волновая функция этого состояния была собственной функцией соответствующего оператора. Таким образом, для того чтобы две наблюдаемые могли иметь одновременно точные значения необходимо, чтобы операторы этих наблюдаемых имели общие собственные функции. Как было показано ранее, это возможно лишь в том случае, если операторы этих наблюдаемых коммутируют. В противном случае наблюдаемые могут быть совместно измерены лишь с некоторой погрешностью. Определим границы этой погрешности.
Пусть ![]() и
и ![]() операторы
динамических переменных, причём
операторы
динамических переменных, причём
![]() (1.42), где
(1.42), где ![]() , так же как
, так же как ![]() и
и ![]() является
эрмитовым оператором. Введём операторы отклонения от среднего
является
эрмитовым оператором. Введём операторы отклонения от среднего ![]() и
и ![]() .
Очевидно, что эти операторы эрмитовы, а их коммутатор равен правой части
выражения (1.42):
.
Очевидно, что эти операторы эрмитовы, а их коммутатор равен правой части
выражения (1.42):
![]() (1.43).
(1.43).
Рассмотри заведомо неотрицательное выражение
![]() (1.44), в котором
(1.44), в котором ![]() - произвольное
действительное число. Используя условие эрмитовости, выражение (1.44) можно
преобразовать следующим образом
- произвольное
действительное число. Используя условие эрмитовости, выражение (1.44) можно
преобразовать следующим образом
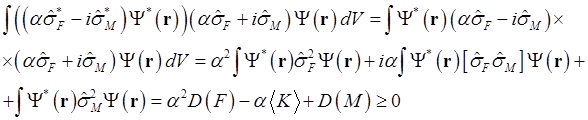 (1.45), где
(1.45), где ![]() и
и ![]() . Полученное в правой части формулы (1.45)
выражение представляет собой квадратичный трёхчлен относительно переменной
. Полученное в правой части формулы (1.45)
выражение представляет собой квадратичный трёхчлен относительно переменной ![]() . Для того, чтобы он был неотрицательным
при любых значениях
. Для того, чтобы он был неотрицательным
при любых значениях ![]() , должно выполняться
условие
, должно выполняться
условие ![]() . Тогда окончательно получаем
. Тогда окончательно получаем
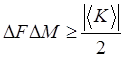 (1.46), где
(1.46), где ![]() и
и ![]() - среднеквадратичные флуктуации наблюдаемых
F и M:
- среднеквадратичные флуктуации наблюдаемых
F и M:
![]() (1.47).
(1.47).
Рассмотрим коммутационные соотношения для проекций
операторов координаты r и импульса ![]() . Очевидно, что разноимённые проекции этих
операторов коммутируют, так как они действуют на разные переменные. Для x- проекций этих операторов получим
. Очевидно, что разноимённые проекции этих
операторов коммутируют, так как они действуют на разные переменные. Для x- проекций этих операторов получим
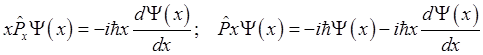
и следовательно
![]() (1.48).
(1.48).
Те же правила коммутации, очевидно, имеют место и для y- и z- проекций операторов координаты и импульса. Сравнивая выражения (1.48) и (1.42), с учётом (1.47) получим соотношения неопределённости для координаты и импульса
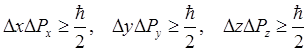 , (1.49)
, (1.49)
где ![]() - среднеквадратичные
флуктуации соответствующих величин. Таким образом, координата частицы и
одноимённая проекция её импульса могут быть известны одновременно только с
некоторой неточностью, определяемой соотношением (1.49).
- среднеквадратичные
флуктуации соответствующих величин. Таким образом, координата частицы и
одноимённая проекция её импульса могут быть известны одновременно только с
некоторой неточностью, определяемой соотношением (1.49).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.