Математический аппарат квантовой механики. Самосопряжённые (эрмитовы) операторы. Собственные функции и собственные значения, страница 2

В частном случае  из последнего выражения получим

                                        (1.20).

Подынтегральное выражение в формуле (1.20) неотрицательно, а сам интеграл не равен 0, откуда следует , что и доказывает действительность собственных значений. С учётом последнего при   из (1.19) получим условие ортогональности (1.16). В заключение, отметим без доказательства, что волновые функции вырожденных состояний вообще говоря не ортогональны, но из них всегда могут быть построены линейные комбинации, которые будут удовлетворять условию ортогональности.

Собственные функции , принадлежащие дискретному спектру собственных значений, могут быть нормированы на единицу. Добавляя к (1.16) условие нормировки (1.2), получим условие ортонормированности собственных функций

                                          (1.21)

где 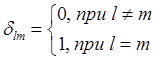   - символ Кронекера.

Собственные функции линейного самосопряженного оператора являются линейно независимыми. Это означает, что равенство будет иметь место только, если все С_k=0. В этом нетрудно убедиться, если умножить это равенство на при произвольном значении l , проинтегрировать по всему пространству и учесть условие (1.21). В теории линейных операторов доказывается, что собственные функции эрмитовых операторов не только линейно независимы, но образуют полную систему линейно независимых функций. Последнее утверждение означает, что произвольную квадратично интегрируемую волновую функцию , можно представить в виде линейной комбинации собственных функций эрмитового оператора:

                                             (1.22)

(сравните с разложением (1.7).  Считая волновую функцию  нормированной на 1 и подставляя в условие нормировки (1.2) разложение (1.22) получим критерий полноты набора собственных функций

и окончательно

                                                   (1.23).

Для нахождения коэффициентов разложения (1.22), домножим это разложение на функцию  и проинтегрируем по всему пространству:

.

Окончательно получим

                                          (1.24).

Полученные для дискретного спектра выражения, после небольшой модификации могут быть распространены и на случай непрерывного спектра собственных значений оператора. Особенностью собственных функций , принадлежащих непрерывному спектру собственных значений , является то, что интеграл от квадрата их модуля расходится

В таком случае значение интеграла 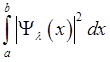будет пропорционально (но не равно!) вероятности нахождения частицы на отрезке [a,b]. Ясно также, что отношение вероятности пребывания частицы на любом конечном участке пространства к вероятности его пребывания во всем пространстве равно нулю. Это означает, что в состояниях непрерывного спектра частица находится на бесконечности.

Для функций непрерывного спектра вместо выражения (1.21) получим условие ортонормированности в виде

                                    (1.25), где  - дельта-функция Дирака. Дельта-функция Дирака задаётся условием

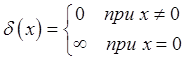                                           (1.26)

и интегрально нормируется на единицу

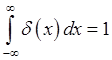                                                 (1.27).

Разложение произвольной функции по полному набору собственных функций оператора с непрерывным спектром даётся формулой

                                          (1.28), а условие полноты приобретает вид

                                                  (1.29).

При этом коэффициенты разложения  в формуле (1.28) по-прежнему определяются формулой (1.24) при соответствующей замене нижних индексов.

В заключение докажем две небольшие, но очень важные теоремы.

Теорема 1. Если операторы имеют общие собственные функции, то они коммутируют.

Пусть  - общая собственная функция операторов и , так что  и .

Обозначим величину , которая называется коммутатором операторов и  как . Тогда

.

Такой же результат будет получен и при действии коммутатора на произвольную функцию, что становится очевидным, если разложить эту функцию по набору общих собственных функций указанных операторов. Это означает, что данные операторы коммутируют – теорема доказана.

Теорема 2. Если операторы коммутируют, то они имеют общие собственные функции.

Пусть  и пусть - собственная функция оператора с собственным значением g, т.е.  Подействуем на обе стороны равенства слева оператором . Тогда по условию теоремы получим

Из последнего равенства видно, что функция также является собственной функцией оператора  , причём с тем же собственным значением g. Если это значение является невырожденным, то функции  и  должны совпадать с точностью до постоянной, т.е. , где k – константа. Таким образом, собственная функция оператора является одновременно и собственной функцией оператора , что и требовалось доказать. Заметим, что при наличии вырождения данная теорема, вообще говоря, не верна. Однако из собственных функций, принадлежащих одному собственному значению всегда можно построить линейные комбинации, которые будут общими собственными функциями коммутирующих операторов.