Математический аппарат квантовой механики. Самосопряжённые (эрмитовы) операторы. Собственные функции и собственные значения

Лекция №2.

План лекции:

математический аппарат квантовой механики.

Ключевые слова:

оператор

самосопряжённые (эрмитовы) операторы собственные функции и собственные значения

Математический аппарат квантовой механики.

Отличительной особенностью квантовой механики является то, что её объекты принадлежат микромиру, в то время как о состоянии этих объектов судят с помощью макроскопических приборов. Эти приборы в отличие от измеряемых ими объектов подчиняются законам классической физики и могут измерять лишь «классические» характеристики. Поэтому как в классической, так и в квантовой механике присутствуют одни и те же динамические переменные. Однако, динамические переменные квантовой механики, как следует из принципа неопределённости, в общем случае, не имеют определённого значения и поэтому не могут непосредственно фигурировать в уравнениях. В то же время одной из задач квантовой теории является определение спектра собственных значений наблюдаемой, а также вероятностей их получения и среднего значения наблюдаемой. Для того, чтобы понять особенности построения математического аппарата квантовой механики рассмотрим частный случай, относящийся к процедуре вычисления среднего значения координаты. Для одномерного случая эта процедура состоит в вычислении интеграла (1.3).  Перепишем его в симметричном виде:

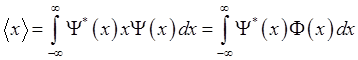                           (1.8), где в последнем интеграле . Естественно предположить, что среднее значение произвольной наблюдаемой F определяется сходным интегральным выражением, билинейным по волновой функции. Представим это выражение по аналогии с (1.8) в виде:

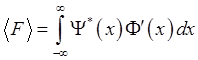                                           (1.9), где Φ′(x) – функция, полученная путём некоторого преобразования волновой функци Ψ(х), причём конкретный вид этого преобразования должен, очевидно, зависеть от наблюдаемой. Это преобразование можно обозначить символом , который называется оператором наблюдаемой F (здесь и далее признаком оператора будет наличие значка ˆ над символом). Тогда можно записать

                                                (1.10)

и выражение для среднего значения наблюдаемой приобретёт вид:

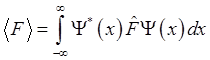                                        (1.11).

В частности, оператор координаты, как следует из сравнения выражений (1.11) и (1.8) сводится к умножению на координату. Операторы других наблюдаемых ещё предстоит установить. Однако прежде рассмотрим некоторые свойства операторов.

Будем считать, что оператор всегда действует на выражение, стоящее справа от него. Введём понятия суммы и произведения операторов. Суммой (произведением) операторов  и  называются операторы , которые удовлетворяют условиям

                                                                         (1.12).

Заметим, что порядок действия операторов в произведении не является произвольным. В отличие от чисел, операторы нельзя переставлять местами, так как в общем случае . Если же порядок действия операторов не влияет на результат и , то говорят, что операторы  и  коммутируют.

Все операторы квантовой механики в силу принципа суперпозиции должны быть линейными, в дальнейшем будут рассматриваться только такие операторы. Оператор  называется линейным, если при действии на волновую функцию  вида он удовлетворяет условию

                                 (1.13).

Каждому оператору можно поставить в соответствие эрмитово сопряжённый ему оператор , который определяется равенством

                                   .

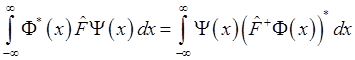Оператор называется эрмитовым (самосопряжённым), если . В интегральном виде условие эрмитовости оператора имеет вид

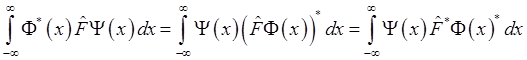         (1.14)

При действии оператора на функцию может оказаться так, что в результате будет получена та же самая функция, умноженная на константу:

                                              (1.15).

Функция, удовлетворяющая условию , называется собственной функцией, а постоянная λ – собственным значением оператора . У операторов имеется множество собственных функций  и соответствующих этим функциям собственных значений λ. Совокупность собственных значений образует спектр собственных значений оператора.  Этот спектр может быть непрерывным или дискретным. В первом случае собственные значения образуют непрерывный континуум, во втором – счётное множество значений λ_k, где k=1,2,… . Если одному собственному значению λ  принадлежит несколько собственных функций , где α=1,2, …,s, то собственное значение λ является s–кратно вырожденным.

Можно показать, что собственные значения эрмитовых операторов являются действительными, а собственные функции, принадлежащие различным собственным значениям, удовлетворяют условию ортогональности

                              (1.16), где  и  собственные функции оператора , принадлежащие соответственно собственным значениям и . Для доказательства этого утверждения рассмотрим выражения

                           (1.17)

                         (1.18), в которых использовано условие (1.15). Проводя над (1.18) операцию комплексного сопряжения и вычитая его из (1.17) получим с учётом условия эрмитовости оператора

                                                                         (1.19).