Линейный гармонический осциллятор. Операторы рождения и уничтожения. Энергетический спектр осциллятора. Энергия нулевых колебаний, страница 2

Теперь, когда энергия основного состояния определена, можно записать общую формулу квантования энергии линейного гармонического осциллятора:

     .                       (2.44)

Схема энергетических уровней осциллятора представлена на рис.7. Минимальная энергия осциллятора, так называемая энергия нулевых колебаний оказалась равной ½ ħω . Квантовый осциллятор, в отличие от классического, не может находиться в покое в положении равновесия. Как уже отмечалось ранее, наличие у связанной системы, находящейся в основном состоянии ненулевой кинетической энергии обусловлено соотношениями неопределенности. 

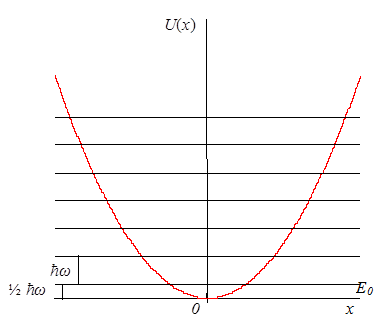
Рис.7. Схема уровней энергии осциллятора.

Теперь найдем волновые функции стационарных состояний. Начнем с отыскания волновой функции основного состояния. Для этого воспользуемся выражением (2.42), подставив в него оператор â из формулы (2.32):

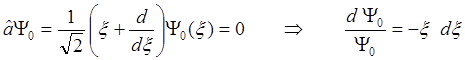.                       (2.45)

Решая последнее уравнение имеем

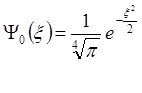                   ,                                              (2.46)

при этом в (2.46) использовано также условие нормировки волновой функции:

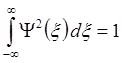           .                                              (2.47)

Теперь волновые функции более высоких энергетических состояний можно найти, последовательно действуя оператором рождения â⁺ на волновую функцию Ψ₀(ξ). При каждом действии в результате будет получаться волновая функция стационарного состояния, номер которого на 1 больше начального. Правила действия операторов â⁺ и â на волновые функции определяются выражениями

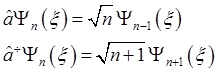                                       (2.48),

в которых все волновые функции нормированы на 1. Для того, чтобы убедиться в справедливости последних двух формул достаточно возвести обе части равенств в квадрат и проинтегрировать полученные выражения по всему пространству.  Так, в частности, исходя из первой формулы получим:

.

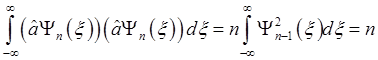Преобразуем теперь левую часть формулы, используя свойство эрмитовой сопряженности операторов â⁺ и â  и формулу (2.34):

 .

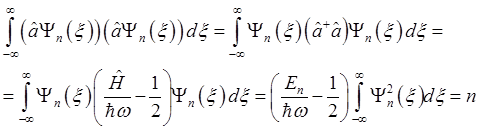Аналогичным образом проверяется справедливость второго выражения в (2.48). Получим теперь выражение для волновой функции состояния с n=1:

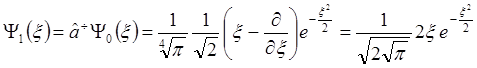.          (2.49)

Можно показать, что в общем случае волновые функции стационарных состояний описываются выражением:

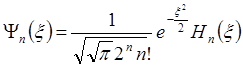    ,                                                     (2.50)

где H_n(ξ) – полиномы Эрмита, которые можно найти с помощью формулы:

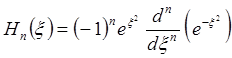     .                                                      (2.51)

В частности для состояния с n=2 нетрудно получить:

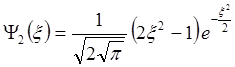  .                                                        (2.52)

Волновые функции (2.50) обладают определенной четностью, что обусловлено симметрией потенциала.

Сравним распределение вероятности координаты у квантового и классического осциллятора. Классический осциллятор может находиться только на отрезке ограниченном поворотными точками, координаты которых находятся из условия  E_n=U(ξ_n). Из этого условия получим, что . Классический осциллятор  больше всего времени проводит именно в поворотных точках.

Иная ситуация имеет место в случае квантового осциллятора, распределение плотности вероятности координаты которого для нескольких состояний показано на рис.8 (на рис.8б  для сравнения приведено аналогичное распределение для классического осциллятора).  В основном состоянии наиболее вероятной координатой осциллятора является точка 0 (рис.8а). За

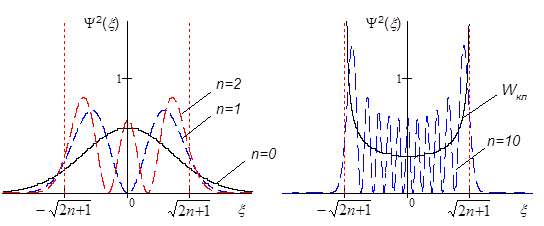
а)                                                     б)

Рис.8. Распределение вероятности координаты осциллятора

в состояниях с разным квантовым числом n

пределами поворотных точек, которые обозначены на рисунках вертикальными  пунктирными линиями, функция плотности вероятности отлична от 0, хотя и быстро затухает по мере удаления от классических границ движения. С ростом квантового числа n распределение вероятности постепенно приближается к классическому (рис.8б).