Линейный гармонический осциллятор. Операторы рождения и уничтожения. Энергетический спектр осциллятора. Энергия нулевых колебаний

Лекция № 10.

Линейный гармонический осциллятор.

Ключевые слова:

операторы рождения и уничтожения энергетический спектр осциллятора

энергия нулевых колебаний

Частица движется в поле 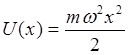, её энергия Е>0. Движение финитное, поэтому энергетический спектр должен быть дискретным.

Для отыскания волновых функций и энергетического спектра частицы надо решить стационарное уравнение Шредингера. Однако в данном случае мы не будем решать дифференциальное уравнение, а найдем решение другим путем. Прежде всего, в гамильтониане

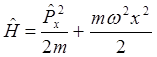                                                                           (2.29)

перейдем к безразмерным величинам: координате  ?  и импульсу  , которые определим следующим образом

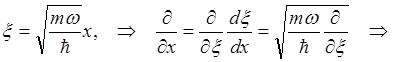
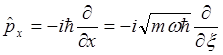
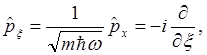
Коммутационные соотношения для введенных безразмерных операторов координаты и импульса с учетом (1.48) имеют вид

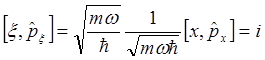                                         ,                       (2.30)

а гамильтониан (2.29) можно представить в виде

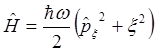                                                                           (2.31)

Введём два новых, эрмитово сопряженных друг другу  оператора:

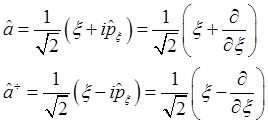                                   (2.32)

                                                                     

С учётом (2.30) для них нетрудно получить

                                                                              (2.33)

С помощью этих операторов гамильтониан системы можно представить в виде

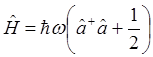                 .                                                          (2.34)

Найдем правила коммутации оператора Гамильтона с операторами  и :

                  (2.35)

и аналогично

  .                                  (2.36)

Обратимся теперь к уравнению Шредингера и пусть волновая функция ?_Е – собственная функция оператора Гамильтона, принадлежащая собственному значению Е

   .                                              (2.37)

Подействуем слева оператором  â на обе стороны равенства:

   .                                  (2.38)

Меняя в левой части выражения порядок действия операторов, с помощью коммутационных соотношений (2.35) получим:

            .           (2.39)

Из последнего равенства следует, что, стоящее в скобках выражение (âΨ_Е) также представляет собой собственную  функцию оператора Гамильтона, соответствующую  значению энергии Е-hω.  Иными словами, оператор â, действуя на волновую функцию некоторого стационарного состояния, преобразует её в волновую функцию другого стационарного состояния, энергия которого оказывается меньше исходной на величину кванта энергии hω .

Аналогичным образом можно показать, что оператор â⁺ добавляет к энергии состояния квант колебания hω.

                                              (2.40)

Операторы â⁺ и â  называют операторами рождения и уничтожения, они соответственно порождают и уничтожают один квант энергии. Действуя последовательно n раз  оператором â⁺  можно получить

                                             (2.41)

Из сказанного выше и полученных формул следует, что уровни энергии осциллятора расположены эквидистантно – расстояния между любыми двумя соседними уровнями одинаковы и равны  hω . Энергетический спектр осциллятора ограничен снизу (Е>0). Для отыскания правила квантования энергии достаточно найти энергию основного состояния. Начнем нумерацию уровней с 0 и подействуем на волновую функцию основного состояния ?₀ оператором  â  . Так как состояния с энергией меньше, чем Е₀ не существует, то результат окажется равным 0. Этот результат, очевидно, не изменится, если дополнительно подействовать на полученное выражение оператором â⁺. Итак

     .           (2.42)

Принимая во внимание формулу (2.34), получим:

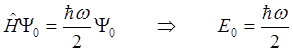            .                       (2.43)