Изучение оборотного маятника (Лабораторная работа № 1_9)

Работа № 1-9 ИЗУЧЕНИЕ ОБОРОТНОГО МАЯТНИКА

ЦЕЛЬ: изучить свойства оборотного маятника, определить ускорение свободного падения.

ОБОРУДОВАНИЕ: оборотный маятник, секундомер.

ОСНОВЫ ТЕОРИИ

Физический маятник - это произвольное тело, вращающееся вокруг оси, не проходящей через его центр масс. Такое тело имеет положение устойчивого равновесия и способно совершать колебания.

Рассмотрим динамику физического маятника (рис.1). Отклоним маятник от положения равновесия на малый угол  j <<1. Сила тяжести создает возвращающий момент силы:

M = - mgasinj » - mgaj,                           (1)

где a - расстояние между центром масс С и точкой подвеса О.

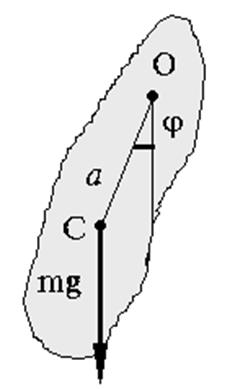
Рис. 1

В соответствии с законом динамики вращательного движения угловое ускорение тела e  равно отношению момента сил М к моменту инерции I.

С учетом того, что , получим уравнение движения для j

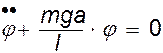                                         (2) 

Мы получили дифференциальное уравнение гармонических колебаний (справедливое для малых углов отклонения j <<1 ) с частотой

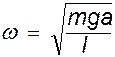                                            (3) 

и периодом Т = 2p/w

Приведенная длина. Для математического маятника (вспомнить определение!) I = ml² и a = l, следовательно

                                           (4) 

Приведенной длиной физического маятника L называется длина математического маятника l, имеющего то же период колебаний. Из уравнений (3) и (4) следует

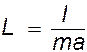                                                (5) 

Момент инерции физического маятника по теореме Штейнера равен

I = I₀ + ma²                                          (6)

где I₀ - момент инерции относительно параллельной оси, проходящей через центр масс.

Тогда

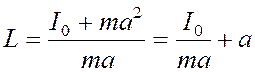                               (7) 

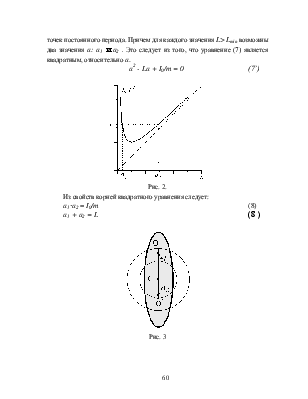
График зависимости L(a) приведен на рис. 2.

При малых a основную роль играет первый член в равенстве (7) (гипербола), а при больших - второй (линейная зависимость). Легко проверить, что приведенная длина L, а следовательно и период (Т²~L) имеют минимум при a= I₀/ma. Это значит, что при подвесе маятника на оси, проходящей на расстоянии I₀/ma от центра масс, он будет иметь минимально возможный период.

Для других приведенных длин L>L_min. возможны два расстояния: a₁ и a₂, дающих эту приведенную длину (и период).

Теорема Гюйгенса. Из формулы (7) следует, что тело, подвешенное на оси, происходящей через любую точку окружности радиусом a имеет один и тот же период (рис.3). Эта окружность является геометрическим местом точек постоянного периода. Причем для каждого значения L>L_min возможны два значения a: a₁ и a₂ . Это следует из того, что уравнение (7) является квадратным, относительно a.

 a² - La + I₀/m = 0                                                                                                     (7’)

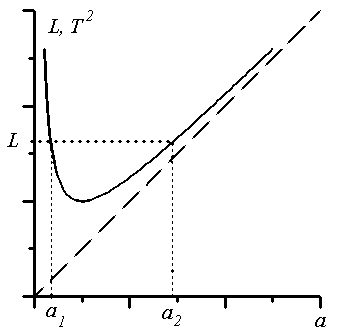
Рис. 2.

Из свойств корней квадратного уравнения следует:

a₁×a₂ = I₀/m                                                                           (8)

a₁ + a₂ = L                                                                                                     (8’)

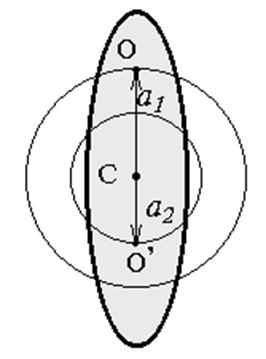
Рис. 3

Это означает что:

1. Если одна окружность имеет радиус меньше, то другая - больше. (Напомним, что совпадение корней дает минимальный период колебаний).

2. Параллельный перенос оси подвеса вдоль прямой, проходящей через центр масс на расстояние, равное приведенной длине L, не изменяет периода колебаний физического маятника. Второе утверждение составляет содержание теоремы Гюйгенса.

Т.е. перенос точки подвеса из точки О в точку О' (рис.3) не изменяет периода колебаний. При этом, как следует из (8’) новая ось попадет на вторую окружность постоянного периода.

Обратное утверждение, строго говоря, неверно: две оси подвеса, дающие одинаковый период, не обязательно находятся на расстоянии L, они могут находиться на одной окружности, т.е. на расстояниях 2a₁ или 2a₂  друг от друга (рис. 3).