Точка O’ на второй окружности называется центром качания для точки подвеса O. И наоборот: точка О будет центром качания для точки подвеса О’.
В наших экспериментах используется оборотный маятник с подвижными частями (рис. 4). На стержне 1 закреплены две опорные призмы - 2 и 2’, на каждой из которых может качаться маятник. Один из грузов 3 закрепляется неподвижно, другой в ходе эксперимента перемещается. Одна из призм (любая) принимается за начало координат и положение подвижного груза 4. отсчитывается от этой призмы независимо от того, на какой подвешен маятник.
При изменении положения грузов изменяются периоды колебаний T1 и T2 на каждой призме. Если при каком-то положении груза периоды совпадают, то расстояние между призмами L будет равно приведенной длине маятника данной конфигурации. Т. е. в наших экспериментах перемещением груза 4 конфигурация маятника “подгоняется” под уже заданную приведенную длину L, а не определяется приведенная длина заданного маятника.
Зная приведенную длину маятника найденной конфигурации и измерив соответствующий период колебаний, можно определить ускорение свободного падения по формуле (4).
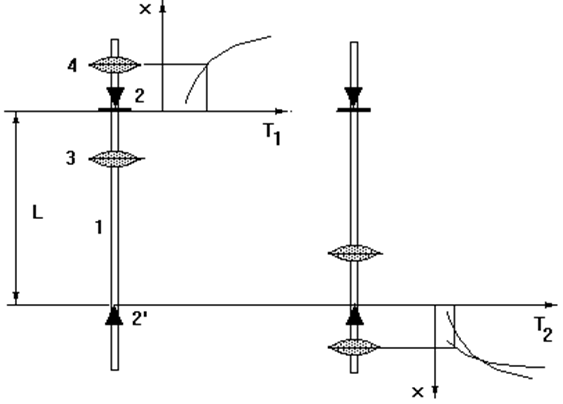
Рис. 4
Примечание: Напоминаем, что совпадение периодов колебаний для двух осей не обязательно дает расстояние L. Однако, если один груз перемещается между призмами, а другой расположен снаружи, то при T1 = T2 обе оси не могут лежать на одной окружности, т.к. в этом случае центр масс маятника должен находиться посередине между призмами.
1. Закрепить неподвижный груз и призмы оборотного маятника в положениях, указанных преподавателем.
2. Измерить расстояние между призмами L.
3. Подвесить маятник на одну из опор, выбранную за начало отсчета, и перемещая подвижный груз вдоль стержня с интервалом 1 см, измерить периоды колебаний T1. Расчеты показывают, что при перемещении груза, находящегося между призмами, период колебаний изменяется мало, поэтому перемещать следует тот груз, который находится вблизи конца стержня.
Результаты занести в таблицу измерений.
Таблица
|
х, см |
|
|
t1, с |
|
|
t2, с |
|
|
T1, с |
|
|
T2, с |
4. Подвесив маятник на другую призму, измерить периоды колебаний T2 для тех же положений подвижного груза.
Примечания:
а) Для измерения каждого периода измерять время не менее 10 полных колебаний.
б) Отклонение маятника должно быть достаточно мало, не более 50.
5. Построить на масштабно-координатной бумаге графики зависимости T1 и T2 от x и определить положение груза x0 , при котором периоды совпадают. (T1 = T2 = T0)
6. Уточнить при помощи графика положение груза и период обращенного маятника: выполнить п.п. 3-5 в окрестности (по обе стороны) точки пересечения графиков определяя периоды по 50 полным колебаниям.
7. Установив длину математического маятника равной приведенной длине, измерить его период колебаний. Сравнить с периодом физического маятника.
8. Определить ускорение свободного падения через период и приведенную длину физического маятника. (Период колебаний записать с четырьмя значащими цифрами).
9. Вывести формулу для погрешности измерения ускорения свободного падения косвенным методом. Оценив предварительно погрешности измерения L и T0 , вычислить погрешность определения величины g.
1. Выведите формулу периода колебаний физического маятника.
2. Дайте определение приведенной длины физического маятника.
3. Сформулируйте и докажите теорему Гюйгенса.
4. Как определяется ускорение свободного падения в данной работе?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.