








уметь использовать методы теории вероятностей и математической статистики при построении и анализе теоретико-вероятностных моделей случайных явлений и процессов, обработке данных наблюдений над экономическими явлениями и процессами.
1.4. Формы контроля
Промежуточная аттестация. Для контроля усвоения данной дисциплины учебным планом предусмотрено:
по дневной форме обучения – экзамен;
по заочной форме обучения – зачет.
Экзаменационная оценка является итоговой по дисциплине и проставляется в приложение к диплому (выписке из зачетной книжки).
Текущий контроль. В течение семестра:
· Студенты дневной формы обучения выполняют 3 индивидуальных домашних задания (ИДЗ) и сдают 2 коллоквиума;
· Для студентов заочной формы обучения предусмотрено выполнение контрольной работы.
Результаты выполнения указанных работ являются основанием для выставления оценок текущего контроля. Выполнение всех работ является обязательным для всех студентов. Студенты, не выполнившие в полном объеме все эти работы, не допускаются кафедрой к сдаче экзамена, как не выполнившие график учебного процесса по данной дисциплине.
|
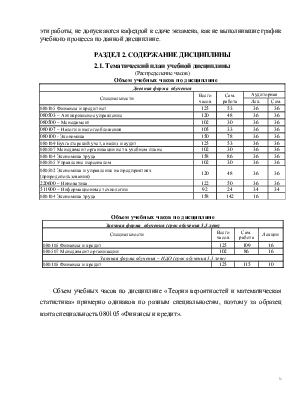
РАЗДЕЛ 2. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ 2.1. Тематический план учебной дисциплины (Распределение часов) Объем учебных часов по дисциплине |
||||
Дневная форма обучения |
||||
|
Специальности |
Всего часов |
Сам. работа |
Аудиторная |
|
|
Лек. |
Сем. |
|||
|
080105 Финансы и кредит нет |
125 |
53 |
36 |
36 |
|
080503 – Антикризисное управление |
120 |
48 |
36 |
36 |
|
080500 – Менеджмент |
102 |
30 |
36 |
36 |
|
080107 – Налоги и налогообложения |
105 |
33 |
36 |
36 |
|
080100 - Экономика |
150 |
78 |
36 |
36 |
|
080109 Бухгалтерский учет, анализ и аудит |
125 |
53 |
36 |
36 |
|
080507 Менеджмент организации нет в учебном плане |
102 |
30 |
36 |
36 |
|
080104 Экономика труда |
158 |
86 |
36 |
36 |
|
080505 Управление персоналом |
102 |
30 |
36 |
36 |
|
080502 Экономика и управление на предприятиях (природопользования) |
120 |
48 |
36 |
36 |
|
220600 – Инноватика |
122 |
50 |
36 |
36 |
|
511900 – Информационные технологии |
92 |
24 |
34 |
34 |
|
080104 Экономика труда |
158 |
142 |
16 |
|
Объем учебных часов по дисциплине |
|||||
Заочная форма обучения (срок обучения 5,5 лет) |
|||||
|
Специальности |
Всего часов |
Сам. работа |
Лекции |
||
|
080105 Финансы и кредит |
125 |
109 |
16 |
||
|
080507 Менеджмент организации |
102 |
86 |
16 |
||
|
Заочная форма обучения – ИДО (срок обучения 5,5 лет) |
|||||
|
080105 Финансы и кредит |
125 |
115 |
10 |
||
Объем учебных часов по дисциплине «Теория вероятностей и математическая статистика» примерно одинаков по разным специальностям, поэтому за образец взята специальность 080105 «Финансы и кредит».
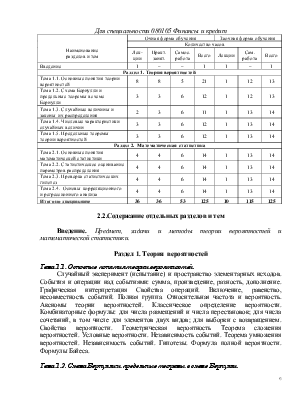
Для специальности 080105 Финансы и кредит
|
Наименование разделов и тем |
Очная форма обучения |
Заочная форма обучения |
|||||
|
Количество часов |
|||||||
|
Лекции |
Практ. занят. |
Самос. работа |
Всего |
Лекции |
Сам. работа |
Всего |
|
|
Введение |
1 |
– |
– |
1 |
1 |
– |
1 |
|
Раздел 1. Теория вероятностей |
|||||||
|
Тема 1.1. Основные понятия теории вероятностей |
8 |
8 |
5 |
21 |
1 |
12 |
13 |
|
Тема 1.2. Схема Бернулли и предельные теоремы в схеме Бернулли |
3 |
3 |
6 |
12 |
1 |
12 |
13 |
|
Тема 1.3. Случайные величины и законы их распределения |
2 |
3 |
6 |
11 |
1 |
13 |
14 |
|
Тема 1.4. Числовые характеристики случайных величин |
3 |
3 |
6 |
12 |
1 |
13 |
14 |
|
Тема 1.5. Предельные теоремы теории вероятностей |
3 |
3 |
6 |
12 |
1 |
13 |
14 |
|
Раздел 2. Математическая статистика |
|||||||
|
Тема 2.1. Основные понятия математической статистики |
4 |
4 |
6 |
14 |
1 |
13 |
14 |
|
Тема 2.2. Статистическое оценивание параметров распределения |
4 |
4 |
6 |
14 |
1 |
13 |
14 |
|
Тема 2.3. Проверка статистических гипотез |
4 |
4 |
6 |
14 |
1 |
13 |
14 |
|
Тема 2.4. Основы корреляционного и регрессионного анализа |
4 |
4 |
6 |
14 |
1 |
13 |
14 |
|
Итого по дисциплине |
36 |
36 |
53 |
125 |
10 |
115 |
125 |
2.2.Содержание отдельных разделов и тем
Введение. Предмет, задачи и методы теории вероятностей и математической статистики.
Тема 1.1. Основные понятия теории вероятностей.
Случайный эксперимент (испытание) и пространство элементарных исходов. События и операции над событиями: сумма, произведение, разность, дополнение. Графическая интерпретация Свойства операций. Включение, равенство, несовместность событий. Полная группа. Относительная частота и вероятность. Аксиомы теории вероятностей. Классическое определение вероятности. Комбинаторные формулы: для числа размещений и числа перестановок; для числа сочетаний, в том числе для элементов двух видов; для выборки с возвращением. Свойства вероятности. Геометрическая вероятность Теорема сложения вероятностей. Условные вероятности. Независимость событий. Теорема умножения вероятностей. Независимость событий. Гипотезы. Формула полной вероятности. Формулы Байеса.
Тема 1.2. Схема Бернулли и предельные теоремы в схеме Бернулли.
Независимость испытаний. Схема последовательных независимых испытаний с двумя исходами и постоянной вероятностью «успеха». Формула Бернулли и следствия из нее. Предельные теоремы в схеме Бернулли: локальная и интегральная теоремы Муавра-Лапласа, следствие для отклонения относительной частоты «успеха». Предельная теорема Пуассона. Условие применимости предельных теорем, пользование таблицами. Обобщение схемы Бернулли - цепи Маркова.
Тема 1.3. Случайные величины и законы их распределения.
Случайные величины (с.в.). Функция распределения с.в. и ее свойства. Дискретные с.в. Ряд распределения и функция распределения дискретной с.в. Примеры дискретных распределений: биномиальное, геометрическое, гипергеометрическое, Пуассона. Непрерывные с.в. Плотность и функция распределения непрерывной с.в. Примеры непрерывных распределений: равномерное, показательное, нормальное. Вероятность попадания нормально распределенной с.в. в заданный промежуток. Правило «трех сигм». Определение функции от случайных величин и закона ее распределения. Определение независимости случайных величин.
Тема 1.4. Числовые характеристики случайных величин.
Математическое ожидание и дисперсия дискретной и непрерывной случайных величин. Свойства и смысл математического ожидания, дисперсии и среднего квадратического отклонения. Математическое ожидание и дисперсия случайных величин, наиболее часто употребляемых в социально-экономических приложениях.
Тема 1.5. Предельные теоремы теории вероятностей.
Неравенство Чебышева. Закон больших чисел, его сущность и роль в социально-экономических исследованиях. Теоремы Чебышева и Бернулли. Центральная предельная теорема и особая роль нормального распределения.
Тема 2.1. Основные понятия математической статистики.
Задачи математической статистики и их связь с задачами теории вероятностей. Квантили и распределения математической статистики. Генеральная и выборочные совокупности. Выборочный метод. Способы образования выборок. Репрезентативность выборки. Способы представления выборочных данных. Полигон и гистограмма относительных частот, эмпирическая функция распределения: определение, свойства и применение.
Тема 2.2. Статистическое оценивание параметров распределения.
Точечное оценивание параметров распределения. Свойства оценок. Интервальное оценивание параметров распределения. Доверительный интервал и доверительная вероятность. Доверительный интервал для генерального среднего и генеральной дисперсии.
Тема2.3. Проверка статистических гипотез.
Понятие статистической гипотезы; нулевая и альтернативная, параметрическая и непараметрическая, простая и сложная гипотезы. Статистический критерий; ошибки первого и второго рода; уровень значимости статистического критерия. Проверка параметрических гипотез. Критерий согласия «хи-квадрат» Пирсона для проверки соответствия гипотетического распределения выборочным данным.
2.4. Основы корреляционного и регрессионного анализа.
Модель взаимосвязи между переменными с учетом случайных факторов. Понятие регрессии и уравнения регрессии. Нахождение коэффициентов линейной регрессии методом наименьших квадратов. Коэффициент корреляции и коэффициенты регрессии. Точечный и интервальный прогноз.
РАЗДЕЛ 3. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
3.1. Темы индивидуальных домашних заданий по дисциплине
ИДЗ 1: События, операции над ними и их вероятности.
ИДЗ 2:Формулы полной вероятности и Байеса. Схема Бернулли.
ИДЗ 3:Случайные величины.
3.2. Список вопросов для подготовки к экзамену (зачету)
1. Испытания и соответствующие им пространства элементарных исходов. События и их графическое представление. Достоверное и невозможное события.
2. Операции над событиями: определения на языке теории множеств и теории вероятностей; графические представления.
3. Включение, равенство и несовместность событий. Полная группа событий.
4. Аксиомы теории вероятностей. Свойства вероятности.
5. Классическое определение вероятности. Гипергеометрические вероятности.
6. Элементы комбинаторики: выборки с возвращением и без возвращения; размещения, перестановки, сочетания и формулы для них.
7. Геометрическое определение вероятности; аналогия с классическим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.