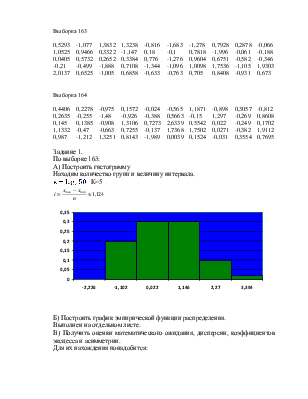





Выборка 163
|
0,5293 1,0525 0,0405 -0,21 2,0137 |
-1,077 0,9466 0,5732 -0,499 0,6525 |
1,3832 0,3322 0,2652 -1,888 -1,005 |
1,3238 -1,147 0,3384 0,7108 0,6858 |
-0,816 0,18 0,776 -1,344 -0,633 |
-1,683 -0,1 -1,276 -1,096 -0,763 |
-1,278 0,7818 0,9604 1,0098 0,705 |
0,7928 -1,996 0,6751 1,7536 0,8408 |
0,2878 -0,061 -0,582 -1,105 -0,931 |
-0,066 -0,188 -0,346 1,9303 0,673 |
Выборка 164
|
0,4406 0,2635 0,145 1,1332 0,987 |
0,2278 -0,255 0,1385 -0,47 -1,212 |
-0,975 -1,48 -0,908 -0,663 1,3251 |
0,1572 -0,926 1,3106 0,7255 0,8143 |
-0,024 -0,388 0,7273 -0,137 -1,989 |
-0,565 0,5663 2,6339 1,7368 0,0039 |
1,1871 -0,15 0,5542 1,7502 0,1524 |
-0,898 1,297 0,022 0,0271 -0,031 |
0,3057 -0,269 -0,249 -0,382 0,3554 |
-0,812 0,8608 0,1702 1,9112 0,7695 |
Задание 1.
По выборке 163:
А) Построить гистограмму
Находим количество групп и величину интервала.
![]() К=5
К=5 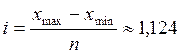
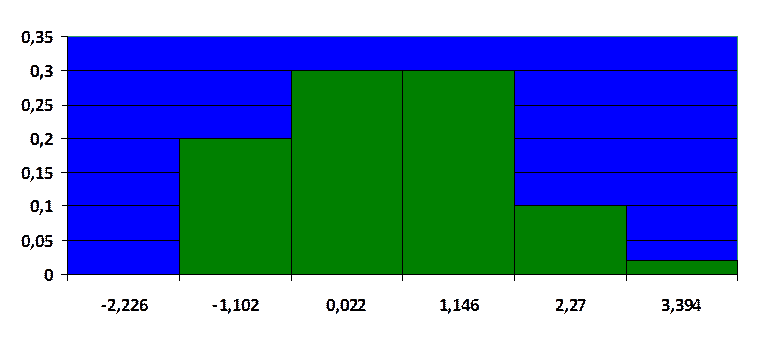
Б) Построить график эмпирической функции распределения.
Выполнен на отдельном листе.
В) Получить оценки математического ожидания, дисперсии, коэффициентов эксцесса и асимметрии.
Для их нахождения понадобится:
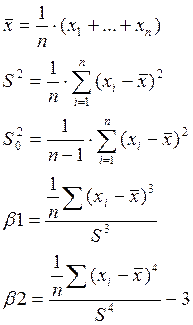
Получается:
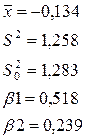
Г) Чтобы проверить гипотезу о нормальности теоретического распределения, применим гипотезы Андерсона-Дарлинга и Жарка-Бера.
Критерий Жарка-Бера:
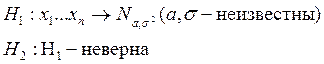
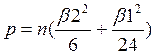
Для расчетов потребуются коэффициенты асимметрии и эксцесса:
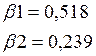
р=1,034
По
ε находим С: ![]() ; С=-2ln ε
; С=-2ln ε
Для ε=0,05 C=5,99
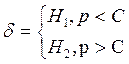
Вывод: Гипотеза Н1 верна.
Критерий Андерсона-Дарлинга:
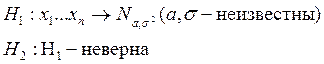
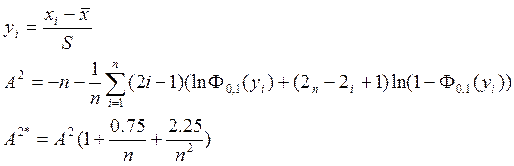
Для расчетов потребуется:
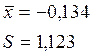
Получаем:
А2=0,452
А2*=0,459
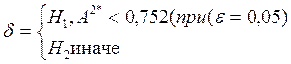
Вывод: Гипотеза Н1 неверна.
Д) Построить доверительные интервалы с уровнями доверия 0,9 и 0,95 для каждого из неизвестных параметров распределения.
Доверительный интервал для а при неизвестном σ2
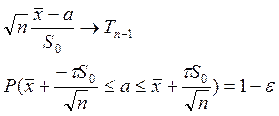
При
![]() τ=1,68 (-0,4032≤ а ≤0,1352)
τ=1,68 (-0,4032≤ а ≤0,1352)
При
![]() τ=2,01 (-0,4561≤ а ≤0,1881)
τ=2,01 (-0,4561≤ а ≤0,1881)
Доверительный интервал для σ2 при неизвестном а:
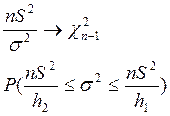
При ![]()
![]() (0,9482≤
(0,9482≤ ![]() ≤1,8538)
≤1,8538)
При ![]()
![]() (0,8958 ≤
(0,8958 ≤![]() ≤1,9937)
≤1,9937)
Задание 2.
По двум выборкам проверить:
А) гипотезу об их независимости
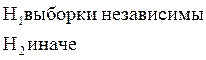
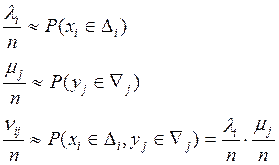
|
выборка 164 |
[-2;-0,5] |
[-0,4;0,5] |
[0,6;2] |
λ |
||
|
[-2;-0,5] |
3 |
5 |
3 |
11 |
||
|
[-0,4;0,5] |
7 |
14 |
4 |
25 |
||
|
[0,6;3] |
6 |
5 |
3 |
14 |
||
|
µ |
16 |
24 |
10 |
50 |
||
Для расчета p воспользуемся формулой:
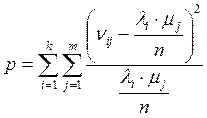
При расчете сумма будет включать в себя девять слагаемых, которые мы опустим.
Получаем:
![]()
ε=0,05
С= h1-ε =9,49
И определяем верную гипотезу
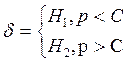
Вывод: Верна первая гипотеза.
Б) Проверим гипотезу однородности в предположении нормальности этих выборок
Критерий Фишера:
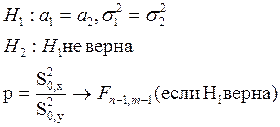
Получаем:
p=1,704
По ε находим f1-ε-квантиль уровня 1-ε Распределения Fn-1,m-1
ε =0,05 f1-ε=1,61
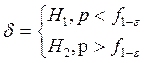
Вывод: Верна первая гипотеза.
Критерий Стьюдента:
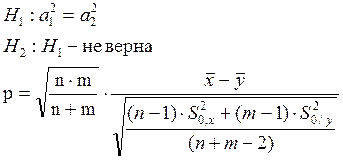
Получаем:
![]()
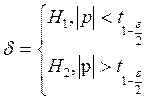
Где ![]() квантиль
уровня
квантиль
уровня ![]() распределения
распределения ![]()
![]() =1,98
=1,98
Вывод: Верна первая гипотеза
В) Проверим гипотезу однородности в отсутствие сведений о нормальности (критерий Вилкоксона, Манна, Уитни)
Проверяется сложная гипотеза
H1 = {![]()
![]() } при
альтернативе H2 = {H1 неверна}.
} при
альтернативе H2 = {H1 неверна}.
Составим из выборок общий вариационный ряд и
подсчитаем U. В общем вариационном ряду ![]() ранги
(номера мест, которые занимают элементы выборки Y в этом ряду).
ранги
(номера мест, которые занимают элементы выборки Y в этом ряду).
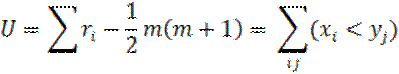
![]()
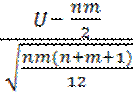
Определяем C по ε
ε =0,05
С=1,96
U=1434
p=1,269
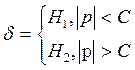
Вывод: Верна первая гипотеза
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.