Методика определения кратковременной электрической прочности газообразных, жидких и твердых диэлектриков

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра электрической изоляции,

кабелей и конденсаторов

ОТЧЕТ

о лабораторной работе № 3

«Исследование электрической прочности диэлектриков»

Работу выполнили студенты группы 3022/1    

           Дементьев М. М.

           Сморгонский А. В.

Соболев Б. С.

Работу приняла преподаватель

Санкт-Петербург, 2005 г.

1.  Цели работы:

-  закрепить теоретические знания физических основ явления пробоя,

-  ознакомиться с методикой определения кратковременной электрической прочности газообразных, жидких и твердых диэлектриков.

2.  Объекты исследования:

-  газообразные, жидкие и твердые диэлектрики.

3.  Перечень оборудования и приборов:

-  измерительная установка для определения электрической прочности,

-  шаровые, игольчатые разрядники.

4.  Программа работы:

4.1  Пробой газов.

Задание:

А) Определить электрическую прочность воздуха в квазиоднородном поле.

Б) Определить электрическую прочность воздуха в неоднородном поле.

Расчетные формулы:

,                ,          

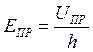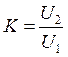
где U₁ – отсчет по шкале вольтметра, U₂ – пробивное напряжение заданного зазора h между сферами, К – коэффициент передачи, U_ПР – пробивное напряжение воздушного зазора h, E_ПР – электрическая прочность воздуха.

Исходные данные:

            d = 6,25 см,

где d – диаметр сферы.

А) Определение электрической прочности воздуха в квазиоднородном поле (шар – шар).

Табл. 1. Результаты эксперимента и их обработка.

Измеренные величины		Табличные значения	Расчетные величины
h, мм	U1, В	U2, кВ	К	UПР, кВ	ЕПР, кВ/мм
1	14,2	3,29	232	3,41	3,41
2	26,1	5,70	218	6,26	3,13
3	33	7,96	241	7,92	2,64
4	41	10,21	249	9,84	2,46
5	48	12,38	258	11,52	2,30

Пример расчета для первой строки:

                                    

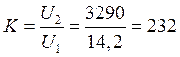
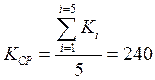
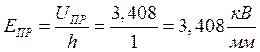
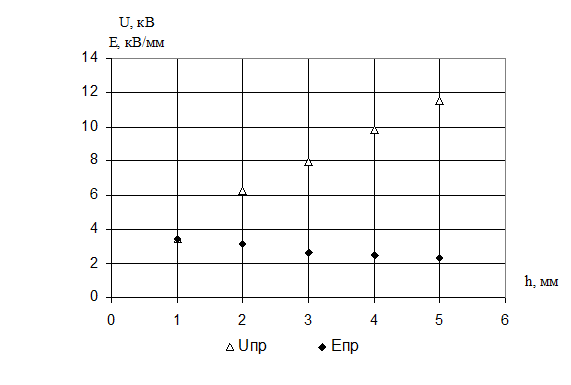
Рис. 1. Графики зависимостей U_ПР = f(h) и E_ПР = f(h) для квазиоднородном поле.

Б) Определение электрической прочности воздуха в неоднородном поле (шар – игла).

Табл. 2. Результаты эксперимента и их обработка.

Пример расчета для первой строки:

          

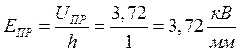
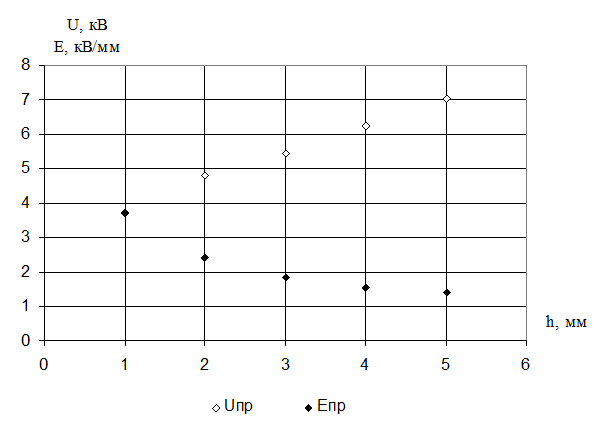
Рис. 2. Графики зависимостей U_ПР = f(h) и E_ПР = f(h) для неоднородного поля.

Выводы по п. 4.1:

            Как мы и ожидали, при увеличении расстояния между электродами (как для случая однородного, так и для случая неоднородного поля), напряжение пробоя увеличивалось, а электрическая прочность воздуха уменьшалась. Это объясняется тем, что между электродами отсутствуют условия для развития лавин вследствие малой длины пробега носителей заряда.

Кроме того, при равных газовых промежутках, электрическая прочность выше в однородном электрическом поле. Это обусловлено тем, что при низком напряжении наблюдается развитие частичных разрядов в виде короны с последующим переходом в искровой разряд и дугу при увеличении напряжения.

4.2  Пробой твердых диэлектриков.

Задание:

А) Исследование влияния структуры электроизоляционных материалов на их электрическую прочность.

Б) Исследование влияния пропитки на электрическую прочность целлюлозных материалов.

В) Исследование числа слоев на электрическую прочность твердых диэлектриков.

Расчетные формулы:

,               

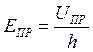А) Исследование влияния структуры электроизоляционных материалов на их электрическую прочность.

Табл. 3. Результаты эксперимента и их обработка (1 слой конденсаторной бумаги).

Толщина образца: h = 10 мкм = 0,01 мм.

Пример расчета для первой строки:

   

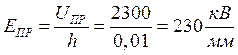
Проведем статистическую обработку результатов. Вычислим среднюю величину электрической прочности диэлектрика:

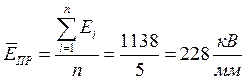
Разброс значений электрической прочности можно охарактеризовать среднеквадратическим отклонением:

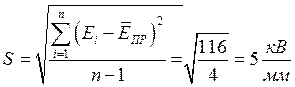
            Чтобы оценить степень однородности материала, вычислим коэффициент вариации:

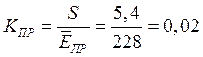
            Определим отклонение средней величины электрической прочности, подчиняющееся распределению Стьюдента:

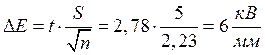
            Окончательное значение электрической прочности с вероятностью 95% находится в пределах:

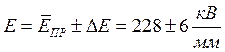
Табл. 4. Результаты эксперимента и их обработка (1 слой лавсановой пленки).

Толщина образца: h = 10 мкм = 0,01 мм.

Пример расчета для первой строки:

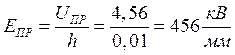
Проведем статистическую обработку результатов. Вычислим среднюю величину электрической прочности диэлектрика:

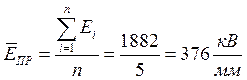
Разброс значений электрической прочности можно охарактеризовать среднеквадратическим отклонением:

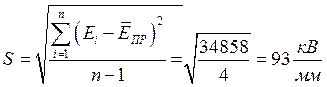
            Чтобы оценить степень однородности материала, вычислим коэффициент вариации:

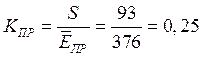
            Определим отклонение средней величины электрической прочности, подчиняющееся распределению Стьюдента:

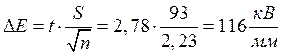
            Окончательное значение электрической прочности с вероятностью 95% находится в пределах:

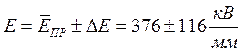
Б) Исследование влияния пропитки на электрическую прочность целлюлозных материалов.

Табл. 5. Результаты эксперимента и их обработка (сухая кабельная бумага).

Толщина образца: h = 120 мкм = 0,12 мм.

Пример расчета для первой строки:

  

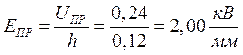
Проведем статистическую обработку результатов. Вычислим среднюю величину электрической прочности диэлектрика:

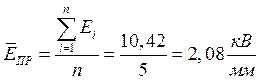
Разброс значений электрической прочности можно охарактеризовать среднеквадратическим отклонением:

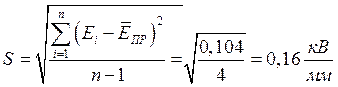
            Чтобы оценить степень однородности материала, вычислим коэффициент вариации:

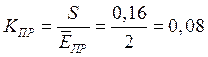
            Определим отклонение средней величины электрической прочности, подчиняющееся распределению Стьюдента:

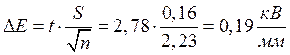
            Окончательное значение электрической прочности с вероятностью 95% находится в пределах:

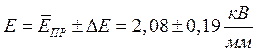
Табл. 6. Результаты эксперимента и их обработка (пропитанная кабельная бумага).

Толщина образца: h = 120 мкм = 0,12 мм.

Пример расчета для первой строки:

 

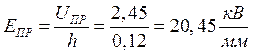
Проведем статистическую обработку результатов. Вычислим среднюю величину электрической прочности диэлектрика:

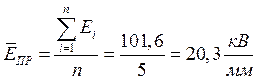
Разброс значений электрической прочности можно охарактеризовать среднеквадратическим отклонением:

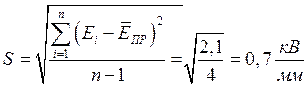
            Чтобы оценить степень однородности материала, вычислим коэффициент вариации:

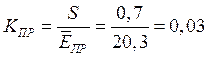
            Определим отклонение средней величины электрической прочности, подчиняющееся распределению Стьюдента:

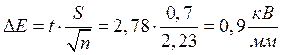
            Окончательное значение электрической прочности с вероятностью 95% находится в пределах:

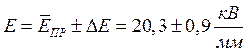
В) Исследование числа слоев на электрическую прочность твердых диэлектриков.

Табл. 7. Результаты эксперимента и их обработка (сухая кабельная бумага).

Толщина образца: h = 10 мкм = 0,01 мм.

Пример расчета для первой строки:

  

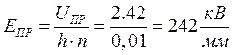
Рис. 3. Графики зависимостей U_ПР = f(n) и E_ПР = f(n)

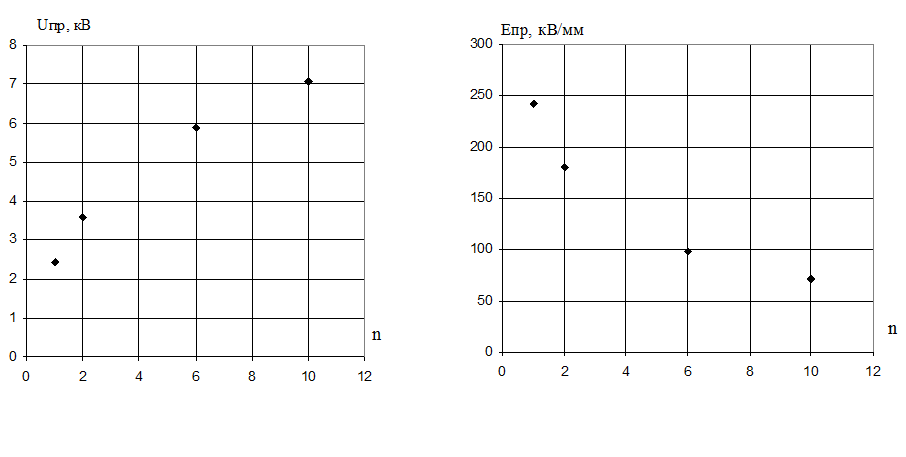
 Выводы по п. 4.2:

            А) В результате эксперимента, мы определили, что конденсаторная бумага обладает меньшей электрической прочностью, чем лавсановая пленка:

       

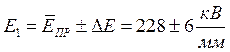
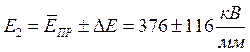
            Кроме того, оказалось, что образцы обладают разной степенью однородности, причем конденсаторная бумага обладает большей однородностью, чем лавсановая пленка:

К₁ = 0,02         К₂ = 0,25