Методические указания к выполнению самостоятельных и практических работ по дисциплине «Математика»

пусть событие С – из 5-ти взятых билетов хотя бы один выигрышный. Это значит, что из 5-ти взятых билетов выигрышных либо 1, либо 2 билета (т. к. выигрышных всего два билета). Пользуясь правилом суммы, находим число исходов, благоприятствующих С:

m_C=m₁+m₂.

Заметим, что m₁ соответствует числу исходов, благоприятствующих событию А, т. е. , а m₂ соответствует числу исходов, благоприятствующих событию В, т. е. . Тогда .

Находим : .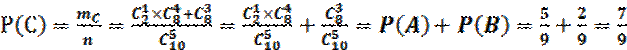

Алгебра событий. Основные теоремы теории вероятностей.

1.  Что понимают под суммой событий?

2.  Что понимают под произведением событий?

3.  Какие события называют независимыми?

4.  Какие события называют зависимыми?

5.  Что такое условная вероятность?

Теорема сложения Вопросы для самопроверки, основные определения и формулы:

6.  Теорема сложения вероятностей:

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Р(А+В) = Р(А) + Р(В )- Р(АВ).

В частном случае, если событие А и В несовместны, то Р(АВ)=0 и формула имеет вид:

Р(А+В) = Р(А) + Р(В),

т. е. вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме их вероятностей.

7.  Теорема умножения вероятностей:

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Р(А×В) = Р(А)×Р_А(В) = Р(В)×Р_В(А).

В частном случае, если события А и В независимы, то  Р_А(В) = Р(В). Р_В(А) = Р(А) и равенство примет вид:

Р(А×В) = Р(А)×Р(В),

т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

8.  Формула полной вероятности:

Рассмотрим событие А, которое может произойти тогда и только тогда, когда произойдет одно из несовместных  событий:  Н₁, Н₂,...,Н_n, образующих полную группу, которые называются гипотезами.

Если известны вероятности гипотез Р(Н₁), Р(Н₂),..., Р(Н_n) и условные вероятности, то вероятность события А вычисляется по формуле:

Эту формулу называют формулой полной вероятности.

9.  Формула Байеса:

Пусть в результате опыта наступило некоторое событие А. Появление события А, как правило, меняет первоначальные вероятности гипотез. В общем случае ставится задача выяснить, какими будут вероятности гипотез Н₁, Н₂,..., Н_n после опыта в предположении, что в результате опыта наступило событие А. Другими словами, условные вероятности Р_А(Н₁), Р_А(Н₂),..., Р_А(Н_n) будет находится по формуле:

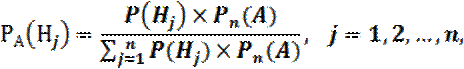
которую называют формулой Байеса, или теоремой гипотез.

Примеры решения задач

Пример 1. В урне 20 белых и 6 черных шаров. Из нее вынимают наугад 2 шара подряд. Найти вероятность того, что шары одного цвета.

Решение. Введем возможные элементарные события:

А₁ – первый взятый шар белый; В₁ – первый взятый шар черный;

А₂ – второй взятый шар белый; В₂ – второй взятый шар черный.

Интересующее нас событие D – шары одного цвета, т. е. или оба белые, или оба черные. Построим событие D:

Заметим, что оба события А₁ и А₂ зависимы так как вероятность любого из них изменяется в зависимости от того, произошло или нет другое событие. То же самое можно сказать и относительно событий В₁ и В₂. Далее, события А₁×А₂ и В₁×В₂ несовместны, т. к. вынимаются из урны только два шара, и они не могут быть одновременно и оба белыми, и оба черными. Поэтому используем теоремы сложения для несовместных событий и умножения для зависимых событий:

Все необходимые вероятности найдем, пользуясь классическим определением вероятности:

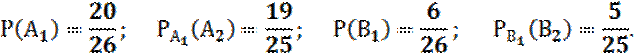
Окончательно имеем:

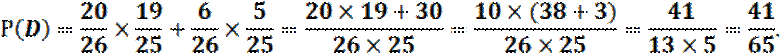
Пример 2. На сборку поступают детали из трех автоматов. Первый дает 20%, второй – 30%, третий – 50% деталей данного типа, поступающих на сборку. Первый автомат дает 0,2% брака, второй – 0,3%, третий – 0,1%. Найти вероятность поступления на сборку бракованной детали.

Решение. Рассмотрим три гипотезы и событие А:

Н₁ – деталь изготовлена первым автоматом;

Н₂ – деталь изготовлена вторым автоматом;

Н₃ – деталь изготовлена третьим автоматом;

А – на сборку поступила бракованная деталь.

Согласно условию задачи, вероятности гипотез будут следующими:

Условные вероятности события А при этих гипотезах соответственно равны:

По формуле полной вероятности,

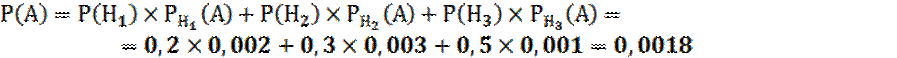
Пример 3. На трех дочерей Алису, Марину и Елену в семье возложена обязанность мыть посуду. Поскольку Алиса старшая, ей приходится выполнять 40% всей работы. Остальные 60% работы Марина и Елена делят поровну. Когда Алиса моет посуду, вероятность для нее разбить, по крайней мере, одну тарелку равна 0,02. Для Марины и Елены эта вероятность равна соответственно 0,03 и 0,04. Родители не знают кто мыл посуду вечером, но они слышали звон разбитой тарелки. Кто, вероятнее всего, мыл посуду?

Решение. В данной задаче даны вероятности разбить хотя бы одну тарелку каждой из дочерей, и, кроме того, устанавливается факт, что тарелка разбита. Это явно указывает на то, что событие А – тарелка разбита, причем это событие уже произошло. Вопрос задачи «подсказывает», какие гипотезы необходимо ввести. Они касаются выбора дочери для мытья посуды:

Н₁  - посуду мыла Алиса;

Н₁  - посуду мыла Марина;

Н₁  - посуду мыла Елена.

Вероятности гипотез легко находятся из условия задачи, касающегося объема выполняемых работ для каждой из дочерей, т. е.

Условные вероятности того, что тарелка будет разбита, даны в задаче для каждой дочери, их нужно только правильно записать.

Теперь в задаче найдены все величины, входящие в формулы полной