Теория оценок в математической статистике

Значения данного интеграла для разных  t вычислил Лаплас и представил их в виде таблицы. Эту таблицу можно найти в любом математическом справочнике.  Поскольку значения этого интеграла зависят от предела  t, то  интеграл от функции Гаусса стали называть функцией Лапласа и обозначать как 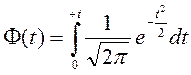. Таким образом, вероятность нахождения неизвестного значения оцениваемого параметра генеральной совокупности можно найти по формуле:

Р=2Ф(t).

Если интервал несимметричен P=Ф(t₂) – Ф(t₁)

Рис. 10.2

Интервальные оценки математического ожидания нормального распределения при известном σ

Пусть генеральная совокупность Х распределена по нормальному закону N(a,σ), причем, параметр σ известен, а параметр a требуется оценить с надежностью P, т.е. найти  P(– ∆x < a <  + ∆x).  

Тогда   P( – ∆x < a < + ∆x)= 2Ф(t), но величина t в данном случае определяется по другой формуле. Т.к. величина t по смыслу – относительное отклонение, т.е. отношение фактического отклонения к стандартному, а для отклонения средних значений от математического ожидания стандартным отклонением является величина   (стандартная ошибка), тогда  .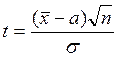

Мы построили для параметра a доверительный интервал (интервальную оценку), левая граница которого 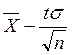, правая – 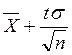, а точность – 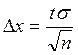. Центр этого интервала находится в точке с координатой , а длина интервала .

Варианты задачи интервального оценивания при известном σ 

Вариант 1

Пусть необходимо найти доверительный  интервал х в котором заключено математическое ожидание a, для заданной доверительной вероятности Р, если стандартное отклонение σ известно.

·  По условию задачи определить .

·  По заданной вероятности,  следует найти функцию Лапласа Ф(t)=Р/2 (вероятность нужно выражать не в процентах, а в виде десятичного числа: 0,95; 0,90 и т.д.).

·  По таблице  Лапласа для данного значения Ф(t) выбирается t.

·  Определить полуширину доверительного интервала по формуле: .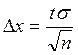

·  Определить границы доверительного интервала: α=–х, β=+х.

Вариант 2

Пусть необходимо найти доверительную вероятность Р того, что математическое ожидание a заключено в доверительном  интервале х , при известном значении σ.

·  По условию задачи определить .

·  По известному значению х определить параметр t по формуле:  .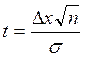

·  По таблице  Лапласа для данного значения t выбирается Ф(t).

·  Определить доверительную вероятность по формуле: Р=2Ф(t).

Вариант 3

Необходимо оценить доверительный интервал для самих значений измеряемого признака. В этом случае 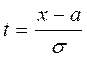 или .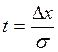

Смысл  сигмового, двухсигмового и трехсигмового интервалов.

Найдем вероятность того, что нормально распределенная величина будет отклоняться от математического ожидания на величину:

·  стандартного отклонения, т.е. х=σ  

P()=2Ф()=2Ф(1)=2·0,3413=0,6826.

·  двойного стандартного отклонения, т.е. х=2σ 

P()=2Ф()= 2Ф(2)=2·0,4772=0,9544

·  тройного стандартного отклонения, т.е. х=3σ 

P()=2Ф()= 2Ф(3)=2·0,49865=0,9973

Из данных уравнений мы делаем вывод,  что при нормальном распределении СВ 68% всех значений СВ лежит в пределах стандартного отклонения. Если отклонение равно двум стандартным отклонениям, то в пределах такого интервала лежит 95% значений СВ. И, наконец, при трехсигмовом интервале 99% всех значений СВ.  Обычно доверительный интервал значений определяют как выборочное среднее плюс-минус два стандартных отклонения.

Интервальные оценки математического ожидания нормального распределения при неизвестном σ. Распределение Стьюдента

Определим теперь интервальную оценку для математического ожидания a, нормально распределенной генеральной совокупности Х в том случае, когда дисперсия генеральная  Dнеизвестна, т.е. построим доверительный интервал для параметра a, если σ неизвестно.

Когда σнеизвестно нельзя пользоваться формулой 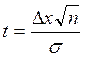. При больших выборках выборочное стандартное отклонение  близко к σ и, в принципе, может быть использовано вместо него, но при малых выборках (n<30) этого сделать нельзя, поэтому вместо случайной величины t используют величину t_p,k, т.е. критерий который зависит не только от величины вероятности Р, но и от количества опытов n. 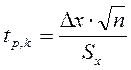, где k=n-1. Данный параметр не зависит от σ!

Разработка теории малой выборки была начата английским статистиком В. С. Госсетом (печатавшимся под псевдонимом Стьюдент) в 1908 г. Он доказал, что в малой выборке действует особый закон распределения.  При оценке результатов малой выборки величина генеральной дисперсии в расчетах не используется. Для определения возможных пределов ошибки пользуются так называемым критерием Стьюдента. Согласно распределению Стьюдента, доверительный интервал зависит как от величины t, а значит,  от вероятности Р, так и от объема выборки  n.  Чем меньше объем выборки, тем более случайным образом, а значит,  менее надежно располагается в данном интервале неизвестный параметр. 

Распределение таких выборок описывается формулой Госсета

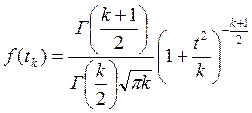
Значения этой функции как видно, зависят от t и k.

k называется числом степеней свободы. Эта величина мало отличается от числа опытов n. Для разных задач  k=n-1, k=n-2, k=2(n-1). При увеличении  k,  а значит,   числа опытов n  значения функции Госсета приближается к значениям функции Гаусса, а график распределения Стьюдента стремится принять вид графика