Изучение затухающих электромагнитных колебаний при помощи осциллографа (Лабораторная работа № 50)

Лабораторная работа  50

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ ПРИ ПОМОЩИ ОСЦИЛЛОГРАФА

Цель работы: изучить один из способов возбуждения и регистрации электромагнитных колебаний в электрической цепи.

Приборы и оборудование: осциллограф С₁ - 73, магазин сопротивлений, катушка индуктивности тип  КИИ, L = 0,01 Гн.

1  ОСНОВНЫЕ СВЕДЕНИЯ

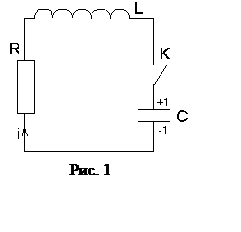
В электрической цепи (рис.1), содержащей емкость, индуктивность и активное сопротивление, могут возникнуть электрические колебания. Если при разомкнутом ключе конденсатор С зарядить до разности потенциалов , а затем замкнуть ключ K, то конденсатор начнет разряжаться через цепочку, состоящую из индуктивности и активного сопротивления R. В цепи возникнет изменяющийся со временем электрический ток (i).

По закону Ома для участка цепи имеем:

,                                                        (1)

где  - мгновенное значение тока в цепи, А;  - активное сопротивление Ом;  - мгновенное значение разности потенциалов между обкладками 1 и 2 конденсатора, В;   - мгновенное значение ЭДС самоиндукции, возникающей в катушке (L) при протекании по ней переменного тока , А.

Так как разность потенциалов между обкладками  конденсатора равна: (j₁ - j₂) = - Q/С, а 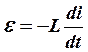, то уравнение (1) примет вид:

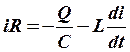                                                    (2)

Разделив это уравнение на L и заменив i на , а  на , получим:

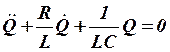.                                                 (3)

Приняв во внимание, что величина, обратная , равна квадрату собственной частоты колебаний контура , то есть

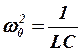,                                                         (4)

и введя обозначение

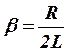, где  - коэффициент затухания, с^-1, уравнению (6.3) можно придать вид:

.                                                   (5)

Уравнение (5) по виду совпадает с дифференциальным уравнением затухающих механических колебаний. При условии, что , то есть 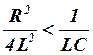, решение уравнения (5) имеет вид:

.                                                (6)

Разделив заряд (6) на емкость С, получим напряжение на конденсаторе:

, где , а .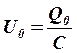

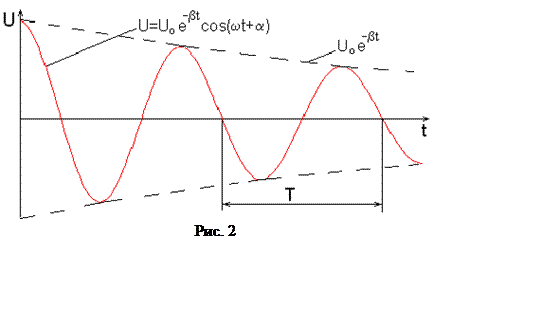
Зависимость изображена на рис. 2.

Чтобы найти силу тока, продифференцируем по времени функцию (6):

.

Умножив правую часть этой формулы на выражение:

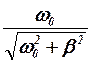 = 1, и введя угол y, определяемый условием: , , можно написать, что

.

Поскольку ,значение  заключено в пределах от  до . Таким образом, при наличии в контуре активного сопротивления сила тока опережает по фазе напряжение на конденсаторе более чем на  (при  опережение составляет ).

Частота затухающих колебаний определяется из выражения:

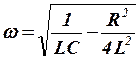.                                                       (7)

Период колебаний определяется из выражения:

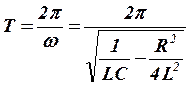.                                                         (8)

При отсутствии активного сопротивления цепи, колебания в контуре являются незатухающими, и период собственных колебаний в контуре определяется по формуле Томсона:

.                                                         (9)

Как видно из рис. 2, амплитуда затухающих колебаний убывает со временем по экспоненте:

.

Промежуток времени (t), в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации ().

Энергия электромагнитных колебаний в начальный момент времени равна энергии заряженного конденсатора. С течением времени энергия колебаний в контуре постоянно уменьшается, так как в процессе прохождения тока (i) в цепи, содержащей активное сопротивление (R), выделяется джоулево тепло. Затухающие колебания принято характеризовать логарифмическим декрементом затухания:

,

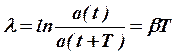где  - амплитуда колеблющейся величины в момент времени t;  - амплитуда через один период.

Кроме логарифмического декремента, колебательный контур часто характеризуют его добротностью:

.

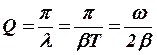При слабом затухании добротность равна отношению энергии (), запасенной в системе в данный момент времени, к убыли этой энергии () за один период колебаний:

.

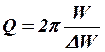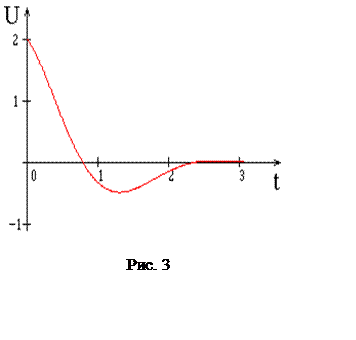
При  или  вместо затухающих колебаний происходит разрядка конденсатора на сопротивлении  (рис. 3) как определяющий процесс.

2  ОПИСАНИЕ  УСТАНОВКИ

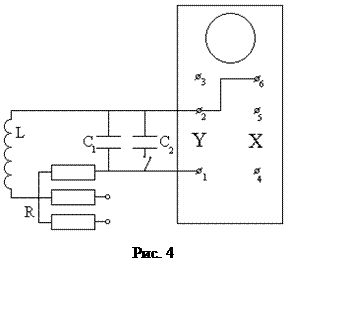Свободные затухающие колебания происходят в контуре (рис. 4), который содержит катушку индуктивности  с высокой добротностью, конденсаторы  и , магазин сопротивлений . Их наблюдают на экране осциллографа, на вертикальный вход U которого подается разность потенциалов с обкладок конденсатора.