того чтобы как можно точнее задать значение корня в первом приближении, следует построить график функции и решить уравнение графически. В данном случае, графическим решением уравнения будет являться абцисса точки пересечения графика функции с осью у=0.
 3) Для нахождения
графического решения воспользуемся режимом трассировки графика. Для
этого следует выделить график и щелкнуть по кнопке
3) Для нахождения
графического решения воспользуемся режимом трассировки графика. Для
этого следует выделить график и щелкнуть по кнопке ![]() панели
инструментов Graph (Графические).
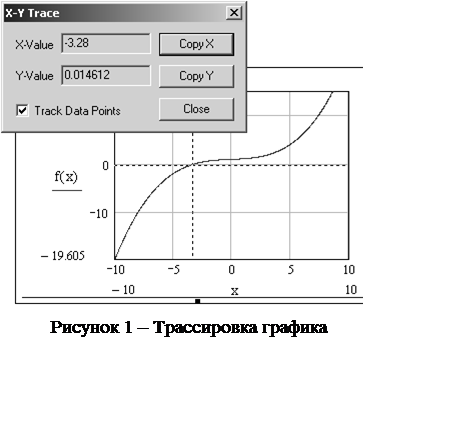
На экране появится диалоговое окно X-Y Trace (рисунок 1).
панели
инструментов Graph (Графические).
На экране появится диалоговое окно X-Y Trace (рисунок 1).
Поместив маркер на какую-либо интересную точку графика, можно примерно определить ее координаты. Однако вручную трудно точно совместить маркер с выбранной точкой графика, поэтому предусмотрен режим слежения за кривой графика. Он реализуется включением опции Track Data Points. При этом перемещение маркера происходит по кривой графика, и можно легко установить его точно на любую точку этой кривой.
После того как был приближенно установлен маркер на точку пересечения графика с осью абсцисс, в поле X-Value будет отражаться графическое решение уравнения. Это значение следует занести в рабочий документ в качестве начального значения переменной поиска корня.
Для этого следует нажать на кнопку ![]() диалогового бокса
X-Y Trace, при этом значение окна будет помещено в буфер
обмена. Далее следует с помощью главного меню [Edit/Paste] или пункта контекстного меню Paste
вставить значение графического решения уравнения в качестве значения переменной
начального поиска.
диалогового бокса
X-Y Trace, при этом значение окна будет помещено в буфер
обмена. Далее следует с помощью главного меню [Edit/Paste] или пункта контекстного меню Paste
вставить значение графического решения уравнения в качестве значения переменной
начального поиска.
4) На следующем этапе следует записать выражения с функцией root и вывести полученное значение.
5) Обязательно следует провести проверку полученного решения.
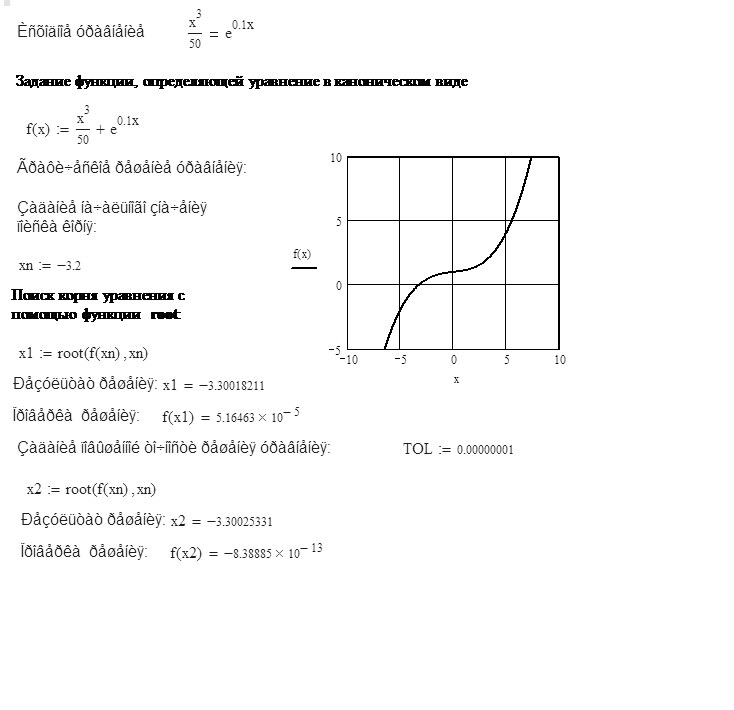 Пример 1.2. Решение
нелинейного уравнения
Пример 1.2. Решение
нелинейного уравнения 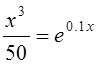
Очень важной характеристикой решения является его точность. В MathCAD можно регулировать величину погрешности решения, изменяя значение специальной системной переменной TOL (от английского tolerance – точность). Строго говоря, TOL – это параметр, определяющий условие прекращения итераций. То есть цикл численного алгоритма поиска решения корня уравнения остановит свою работу и выдаст последнее значение x, если f(x) примет значение меньшее, чем значение параметра TOL.
Изменить величину этой встроенной переменной можно либо при помощи команды Math/Options/Built-in variables/TOL (Математические/ Опции/Системные переменные/TOL), либо выполнив соответствующее переопределение значения TOL непосредственно перед функцией численного решения. По умолчанию значение TOL = 0,001.
На приведенном выше примере можно заметить, как влияет изменение точности решения на точность результата.
1.2 Функция root на интервале приближений
Если необходимо найти корень некоторого уравнения, причем известен интервал, в котором он находится, то проще использовать функцию root с 4 аргументами:
root(f(x), x, a, b) , где f(x) – функция, определяющая уравнение; х – переменная; a и b – границы интервала локализации. Обязательным условием является то, что значения функции на концах интервала должны быть противоположных знаков. Это связано с особенностью реализуемого алгоритма.
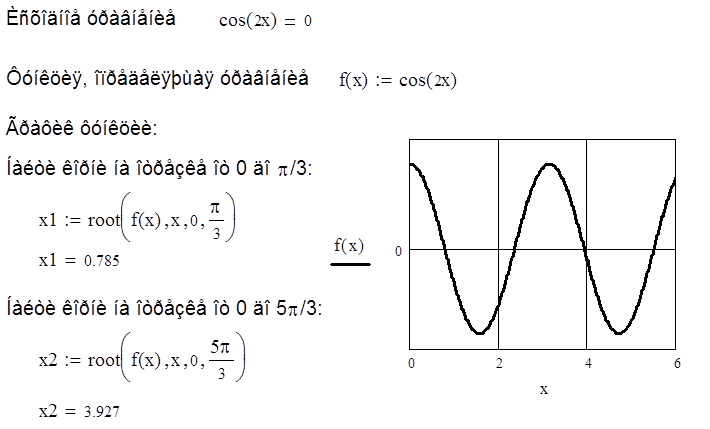 |
Полученный второй результат в рассмотренном примере отличается от первого решения, хотя корень х1 находится в заданном интервале
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.