|
Методические указания для выполнения лабораторных работ по дисциплине ИНФОРМАТИКА |

ст. преп. каф. Информатика
Козыревская А.В.
Лабораторная работа №5
Обработка матриц. Решение систем линейных уравнений матричным способом.
Цель работы: Получить практические навыки по возможностям обработки матриц в MCAD и решению систем уравнений с использованием матриц.
Задание к лабораторной работе.
1. Загрузить среду MCAD и набрать там пояснения
а) Включить русский шрифт. б) Установить тип шрифта Courier New Cyr. в) В появившемся окне набрать рекомендуемый текст.
a. Лабораторная работа №5 в среде MathCAD
b. Выполнил студент(ка) ФИО, группа, шифр
2. Скопировать задание из таблицы 6 и вставить в среду MathCAD
а) Нажать левую кнопку мыши и выделить вариант задания из таблицы 1. б) Скопировать задание в буфер обмена (Правка->копировать).в) Установить курсор( красный крестик) в нужное место и вставить из буфера (Правка->вставить).
3. Задать данную матрицу.
a) Набрать имя матрицы и установить с панели инструментов знак присваивания :=
b) Открыть панель векторов и матриц (значок есть на панели Математика)
c) Выбрать там шаблон матрицы
d) Указать нужное количество строк и столбцов
e) Заполнить шаблон значениями из своего варианта
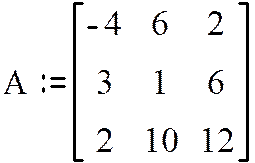
4. Для получения матрицы B, умножим матрицу A на число, равное номеру вашего варианта + 1, так для 14 варианта матрицу A надо умножить на 15.
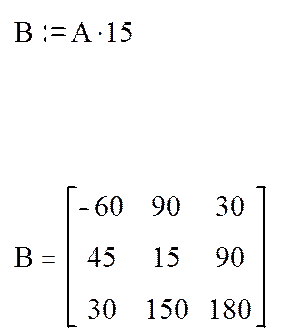
5. Для получения D умножим имеющиеся матрицы между собой.
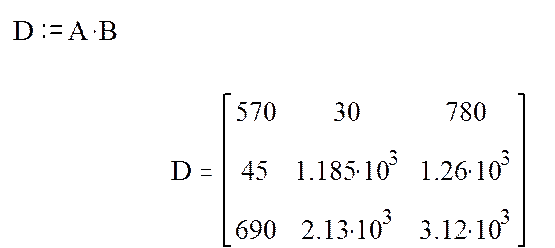
6. Для нахождения дискриминантов матриц выбираем значок модуля на панели матриц, указываем имя и ставим знак равенства.
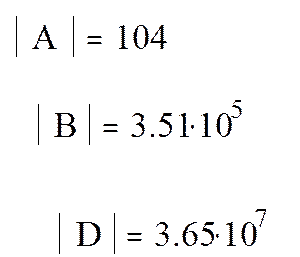
7. Для решения системы линейных уравнений необходимо задать матрицу коэффициентов (коэффициенты брать со знаком, если переменной нет в уравнении, значит коэффициент равен 0), вектор-столбец свободных членов

8. Решение будет найдено по формуле:
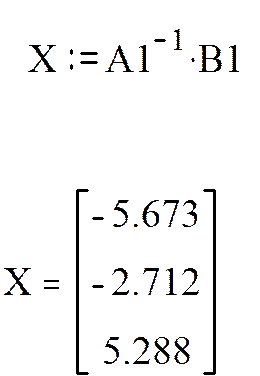
Вариант 1.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
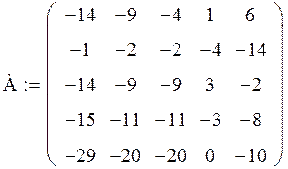
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
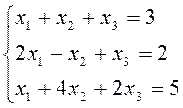
Вариант 2.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
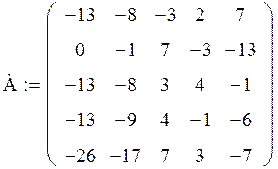
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
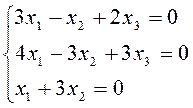
Вариант 3.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
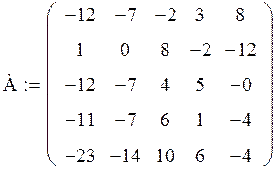
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
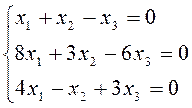
Вариант 4.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
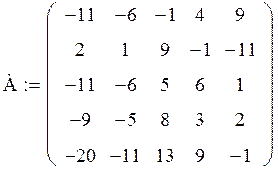
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
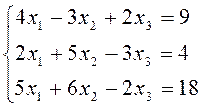
Вариант 5.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
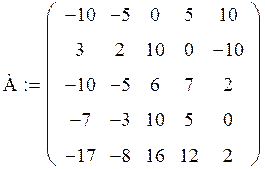
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
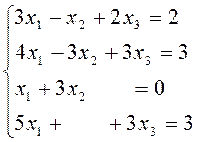
Вариант 6.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
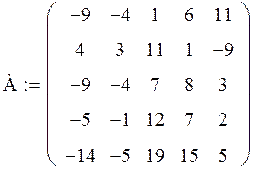
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
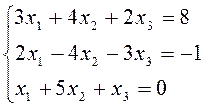
Вариант 7.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
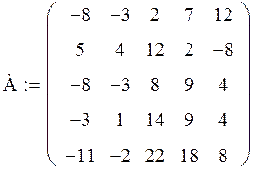
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
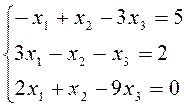
Вариант 8.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
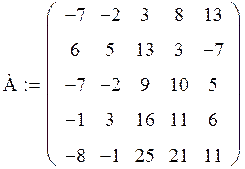
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
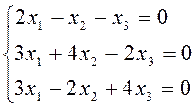
Вариант 9.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
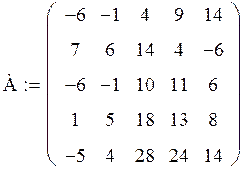
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
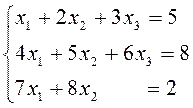
Вариант 10.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
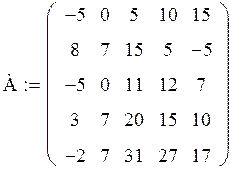
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
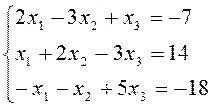
Вариант 11.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
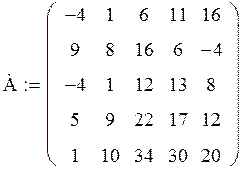
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
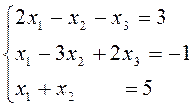
Вариант 12.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
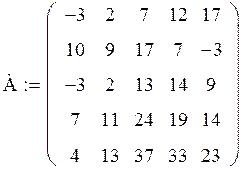
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
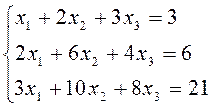
Вариант 13.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
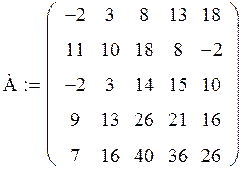
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
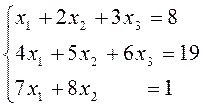
Вариант 14.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
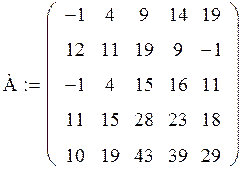
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
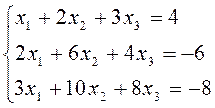
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.