Задание № 6 (Excel)
Решение системы линейных уравнений тремя способами.
![]()
|
На рис. 1 приведены все три способа решения этой системы уравнений. Аналогичным образом
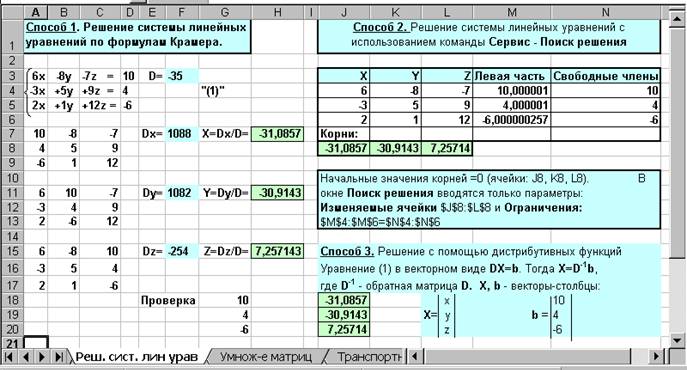 Рис. 1
Рис. 1следует решить эту систему во время выполнения этого задания, повторив оформление решения.
Способ 1. Решение по формулам Крамера.
Ввод текстовой информации и его оформление не должно вызвать затруднений. Технология получения решения и запись уравнений следующие:
1. Для каждого коэффициента уравнения, записанного в ячейки А3:С5 задайте пользовательский формат числа. Для 6 этот формат задается командой: [Ctrl+1] ] (ДО):Формат ячеек ] (Вкл):Число ] Числовые форматы: (все форматы) ] Тип: 0”x”. Т. е. сначала выбирается 0, а после нуля в двойных кавычках вводится х. Аналогично задается пользовательский формат для коэффициентов –8, -7 первого уравнения. Только для –8 тип будет равен 0”y”, а для –7: 0”z =”. Для всех положительных коэффициентов при z тип будет такой: для 9: +0”z =” , для 12: +0”z =”. Какой тип у 5 и 1, легко догадаться.
2. В ячейке F3 по формуле =МОПРЕД(A3:C5) рассчитайте определитель D и такое же имя присвойте этой ячейке.
3. В ячейке F7 по формуле =МОПРЕД(A7:C9) рассчитайте определитель DX и такое же имя присвойте этой ячейке. DX получается заменой первого столбца в матрице D на столбец свободных членов.
4. Аналогично п. 3 рассчитайте определители DY и DZ и результирующим ячейкам присвойте имена определителей.
5. Искомые величины X, Y, Z в столбце H определите по формулам, приведенным слева от них.
6. В ячейках G18, G19, G20 делаем проверку, умножая найденные величины X, Y, Z на их коэффициенты в каждом уравнении.
Способ 2. Решение системы уравнений с помощью команды Сервис ] Поиск решения.
1. Ввести в массив J4:L6 исходные данные – коэффициенты при неизвестных.
2. В массиве М4:М6 вычисляются левые части уравнений с приближенными значениями корней уравнений, равными 0, которые задать в ячейки J8, K8, L8. Достаточно вычислить левую часть первого уравнения, и заполнить введенную формулу в остальные две ячейки. (Не забыть ячейки корней в формулах сделать абсолютными!).
3. В массив N3:N6 ввести свободные члены уравнений.
4. Выполнить команду Сервис ] Поиск решения и в диалоговом окне Поиск решения выполнить следующие настройки.
5. В текстовом поле Изменяя ячейки ввести ячейки $J$8:$L$8, в которых заданы нулевые значения корней.
6. Нажав кнопку Добавить, введите в поле Ссылка на ячейку выражение: $M$4:$M$6, в следующее поле – знак равняется “=”, в текстовое поле Ограничения – выражение $N$4:$N$6 и нажмите кнопку Выполнить (см. рис. 1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.