Определение геометрического фактора по созвездию из 4 – х НКА
Взаимосвязь между точностью определения первичных навигационных
параметров (например, псевдодальностей ![]() )
и точностью координат потребителя СРНС определяется выражением:
)
и точностью координат потребителя СРНС определяется выражением:
![]() (1)
(1)
где σX,Y,Z – погрешности определения координат; KГ – коэффициент геометрии (геометрический
фактор); ![]() - погрешности измерения
псевдодальностей.
- погрешности измерения
псевдодальностей.
Выражение (1) показывает, что соотношение между погрешностями определения первичных и вторичных навигационных параметров зависит только от геометрии взаимного расположения НКА и потребителя.
Погрешности определения псевдодальностей не зависят от геометрии взаимного положения НКА и определяющегося объекта. Полагая, что данные погрешности равновелики и некоррелированы вводится количественная характеристика КГ – коэффициент геометрии.
Коэффициент геометрии определяется следующим образом:
![]() (2)
(2)
где Н – матрица направляющих косинусов; tr(*) – след (trace) матрицы – операция суммирования элементов главной диагонали матрицы.
Таким образом, чтобы найти коэффициент геометрии (геометрический фактор или Dilution Of Precision - DOP) необходимо:
1) составить матрицу наблюдений, которую можно записать в виде
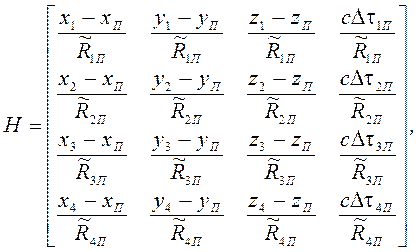 (3)
(3)
где 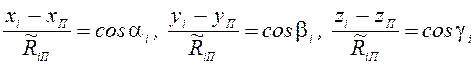 – направляющие косинусы радиус-векторов,
соединяющих потребителя и i – й НС; xi, yi,
zi – координаты i – го НКА, (i = 1 ÷ 4); xП, yП,
zП – координаты потребителя;
– направляющие косинусы радиус-векторов,
соединяющих потребителя и i – й НС; xi, yi,
zi – координаты i – го НКА, (i = 1 ÷ 4); xП, yП,
zП – координаты потребителя; ![]() - псевдодальности между i –м НКА и потребителем (можно
взять из RINEX – файла (тип «observation»));
DτiП
– расхождение шкал времени i –
го НКА и потребителя.
- псевдодальности между i –м НКА и потребителем (можно
взять из RINEX – файла (тип «observation»));
DτiП
– расхождение шкал времени i –
го НКА и потребителя.
Если расхождения шкал неизвестны, то элементы 4 – го столбца матрицы H можно взять равными 1 (единице).
2) транспонировать матрицу H
3) умножить транспонированную матрицу HT на H
4) от произведения HTH взять обратную матрицу (HTH)-1
5) взять след от обратной матрицы и извлечь корень из (HTH)-1
При учёте 4 элементов главной диагонали получается пространственно-временной ГФ.
![]() (4)
(4)
где нижний индекс обозначает номер элемента матрицы (HTH)-1.
При учёте 3 элементов главной диагонали получается пространственный ГФ
![]() (5)
(5)
При учёте 2 элементов главной диагонали получается плоскостной ГФ
![]() (6)
(6)
Временной ГФ можно определить по формуле
![]() (7)
(7)
ЛИТЕРАТУРА
Глобальная спутниковая радионавигационная система ГЛОНАСС / Под ред. В.Н. Харисова, А.И. Перова, В.А. Болдина. – М.: ИПРЖР, 1998. – 400с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.