Лекция 24
УПРОЩЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ ПАРКА-ГОРЕВА ПРИ ИССЛЕДОВАНИИ ЭЛЕКТРОМАГНИТНЫХ ПЕРЕХОДНЫХ ПРОЦЕССОВ В СИНХРОННОЙ МАШИНЕ
Система уравнений позволяет определить все параметры режима, изменяющегося во времени переходного процесса.
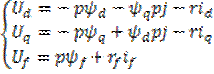 (1)
(1)
Оператор «p» – символ дифференцирования временных функций и как алгебраическая
величина (в области изображений).Рассмотрим два первых уравнений, в которых 4
неизвестных. 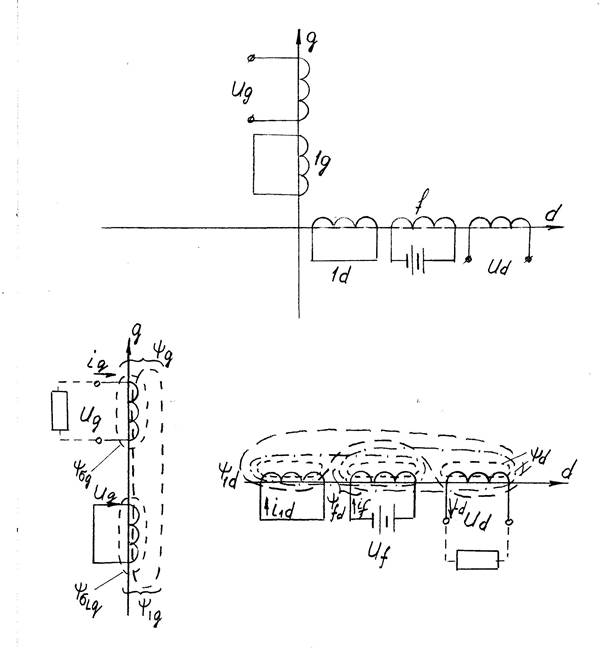
Потокосцепление каждой обмотки можно записать как произведение токов на соответствующие реактивные сопротивления самоиндукции и взаимоиндукции.
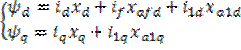 (2)
(2)
Запишем дополнительные уравнения.
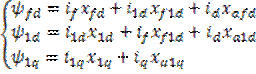 (3)
(3)
Электродвижущая сила,
наводимая в обмотке возбуждения, изменением потокосцепления ![]() будет уравновешиваться напряжением
будет уравновешиваться напряжением ![]() и падением напряжения в отдельном
сопротивлении этой обмотки. В демпферных обмотках ЭДС, наблюдается
потокосцепление
и падением напряжения в отдельном
сопротивлении этой обмотки. В демпферных обмотках ЭДС, наблюдается
потокосцепление ![]() и
и ![]() уравновешивается только падением
напряжения в активном сопротивлении соответствующих контуров.
уравновешивается только падением
напряжения в активном сопротивлении соответствующих контуров.
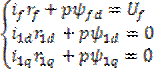 (4)
(4)
Запишем систему
уравнений (4) относительно ![]() ,
, ![]() ,
, ![]() :
:
![]()
Подставляем эти значения в систему
уравнений (3) (получается 3 уравнения с тремя неизвестными) и находим ![]() ,
, ![]() ,
, ![]() , подставим их в систему уравнений
(2), получаем:
, подставим их в систему уравнений
(2), получаем:
![]()
![]()
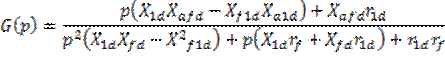
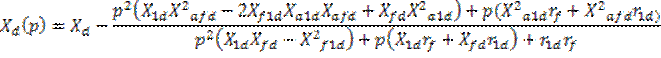
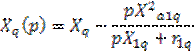
![]() - операторная проводимость.
- операторная проводимость.
![]() ,
, ![]() – операторные сопротивления по
соответствующим осям.
– операторные сопротивления по
соответствующим осям.
Если не учитывать демпферные обмотки, то:
![]()
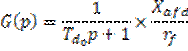
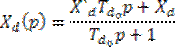
![]() - const времени обмотки возбуждения при разомкнутой обмотки
статора.
- const времени обмотки возбуждения при разомкнутой обмотки
статора.
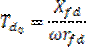
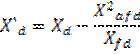
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.