Уменьшение небаланса напряжения, страница 3

Условие, при котором ток в нулевом проводе будет равен нулю, имеет вид:

Следовательно

Реактивная составляющая тока нейтрали

Активная составляющая тока нейтрали

Подстановка числовых значений

 и

Следовательно

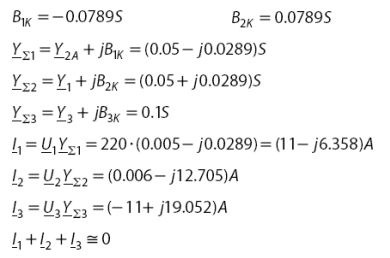
Токовая составляющая нулевой последовательности исключена (Рис.8).

7.   Симметризация трехпроводной нагрузки

7.1.  Симметризация нагрузки соединенной в треугольник

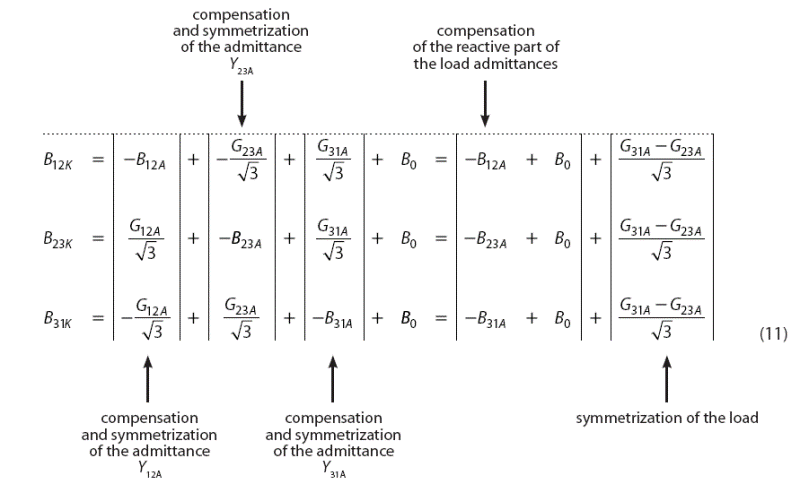
На практике, реактивные проводимости статического компенсатора представляют два процесса одновременно, которые означают симметризацию и компенсацию реактивного тока и потом результирующее значение реактивных проводимостей определяется по (11), где B₀ представляет допустимый уровень не компенсации. Как видно из (11), три проводимости, которые необходимы для компенсации и симметризации реактивного тока, могут быть выражены через реальные и мнимые составляющие проводимостей нагрузки. Первые элементы в правой части представляют составляющие компенсации реактивных проводимостей, необходимых для компенсации мнимой части соответствующих проводимостей нагрузки. Второй элемент представляет составляющие компенсатора, которые необходимы для симметризации реальных частей проводимостей нагрузки. Эти связи ясно определяют, что процесс компенсации также может интерпретироваться как an activity concerning each of the interphase load admittances separately.

Для нагрузки Y_12A  компенсация мнимой части достигается путем параллельного соединения реактивных проводимостей (-B₁₂) следуемых за симметризацией остальной части однофазной нагрузки путем соединения реактивных проводимостей к соответственным напряжениям: (G_12A/ 3) к напряжению U₁₂, и (-G_12A/ 3 ) к напряжению U₃₁ Процесс компенсации нагрузки и показательные диаграммы представлены на Рис.9. Для симметричной системы с питающими напряжениями прямой последовательности такая цепь эквивалентна трем резисторам, соединенным в звезду, каждый из которых имеет активную проводимость G₁₂.

Упомянутые выше рассуждения иллюстрируют хорошо известное правило симметризации Steinmetz, согласно которому любая однофазная нагрузка, подключенная, например, между фазами 1-2 (Рис. 9), может быть симметризирована с помощью реактивных LC- элементов таких величин, чтобы токи удовлетворяли отношения (12).

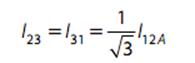
Полученные соотношения (11) преобразовывают любую трехфазную асимметричную нагрузку в симметричную, резистивную или активно-индуктивную нагрузку с определенным уровнем реактивного тока. Для симметричного источника напряжения прямой последовательности полученная цепь эквивалентна (для B₀ = 0) трем, соединенным в звезду резисторам, каждый из которых имеет  проводимость

.

Условие для выбора элементов компенсатора может также быть выражено, как функция фазных реактивных мощностей асимметричной нагрузки                                                              Q1A+Q1K = Q2A+Q2K  = Q3A+Q3K = Q0

Q1A, Q2A, Q3A – реактивные мощности нагрузки,

Q1K, Q2K, Q3K – реактивные мощности компенсатора,

Q0 – предполагаемый уровень некомпенсации.

Для соединенных в треугольник элементов компенсатора междуфазные реактивные мощности могут быть определены согласно соотношениям:

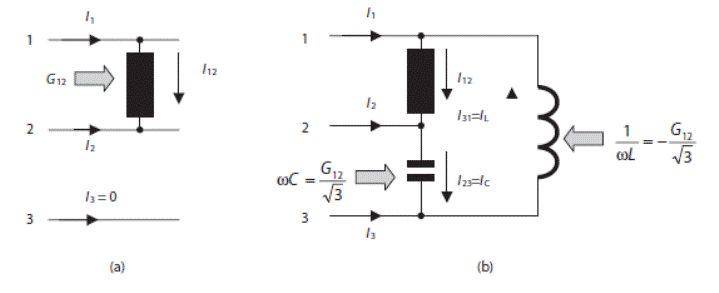
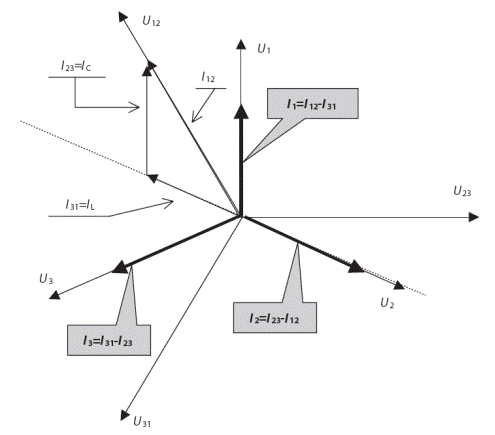
Рис. 9 – a) однофазная система до симметризации;

б) однофазная система с симметризатором;

в) фазная диаграмма, иллюстрирующая процесс симметризации

Пример №3

Для нагрузки из примера 1 – вариант II, реактивные проводимости симметризатора, соединенные в треугольник:

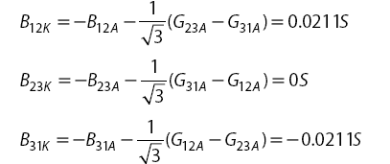
Знак «+» определяет емкостной характер проводимости, знак «-» индуктивный.

Емкость конденсатора, подключенного между фазами 1 – 2, определяется из уравнения:

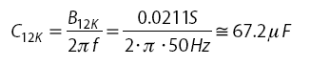
Индуктивность катушки, подключенной между фазами 3 – 1 определяется следующим образом:

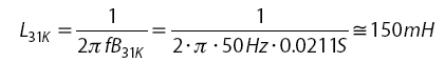
Нагрузка и компенсатор показаны на Рис. 10.

После подключения компенсатора – симметризатора:

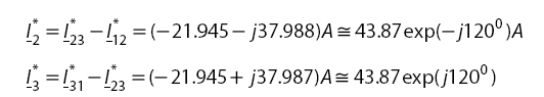
Питающие токи распределительной сети образуют трехфазную симметричную систему.

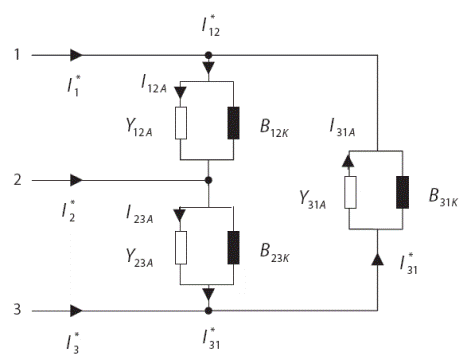
Рис. 10 – Асимметричная нагрузка, соединенная в треугольник с подключенным симметризатором

Напряжения и  Токи трехпроводной сети

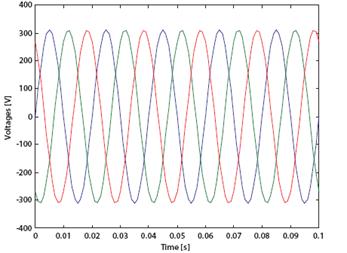
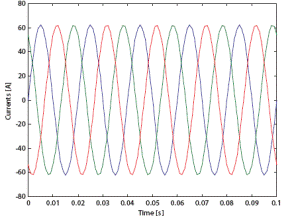
Рис. 11 – Формы кривых напряжений и токов (Пример 3)

7.2 Симметричная нагрузка, соединенная в звезду

Симметризация нагрузки соединенной в звезду осуществляется после трансформации ее в треугольник. Дальнейший процесс выбора параметров симметризатора аналогичен тому, который мы проводили в пункте 7.1.