Уменьшение небаланса напряжения, страница 2

Для устанавливания правил компенсации и симметризации, значения номинальных сопротивлений должны приниматься постоянными, но, в общем, отличаться друг от друга. Но это не исключает возможности их изменения во времени. Эти сопротивления могут рассматриваться как «представление» нагрузки, изменяющейся во времени, но только на конкретных установленных участках времени – мгновенной выборки. Множество таких постоянных значений сопротивлений представляет нагрузку как дискретно-изменяемую во времени.

Компенсация асимметричной нагрузки будет более понятна как компенсация реактивной составляющей прямой последовательности (компенсация реактивной мощности для основной частоты), нулевой последовательности (для трехфазных четырехпроводных систем) и обратной последовательности для основной частоты. Среди различных возможных методов, индуктивно-емкостные системы особо важны. Их практичное применение это известные решения статических следящих компенсаторов.

5.   Свойства компенсаторов - симметризаторов

Симметризация и компенсация основной гармоники реактивного тока это процесс, который на практике представляет собой подключение к реактивной нагрузке реактивных элементов (реакторов, конденсаторов) с такими значениями, чтобы удовлетворить условия:

где  симметричные составляющие асимметричной нагрузки и компенсатора (К), токи соответственно нулевой – (0), прямой – (1) и обратной последовательности;  означает реактивную составляющую прямой последовательности нагрузки токовой компоненты (мнимая часть комплексного числа);  значение реактивного тока, который определяет допустимый уровень не компенсации нагрузки при питании от источника электроснабжения. Таким образом, согласно вышесказанному, процесс компенсации и симметризации реактивного тока (для нулевой и обратной последовательностей) должен быть разделен.

Для нагрузки, изображенной на Рис.4, зависимости характеризующие значения обратной и нулевой последовательностей симметричных составляющих могут быть записаны так (согласно (8)):

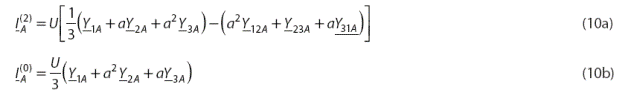
Если выражение (10) не тождественно нулю и уровень асимметрии недопустимо велик, необходима симметризация нагрузки, которая может быть осуществлена путем присоединения симметризационно- компенсационных элементов , подключенных к фазным напряжениям и , подключенных к линейным напряжениям. Проблема решается путем поиска компенсирующих реактивных проводимостей, которые вместе с проводимостями, которые будут компенсироваться, будут образовывать симметричную нагрузку. Далее будет представлена в данной статье зависимость, в которой параметры симметризатора – компенсатора выражаются как функция эквивалентного сопротивления (проводимости) симметризированной/скомпенсированной нагрузки. Это очень важно для создания симметризатора Параметры симметризатора могут быть выражены через другие величины, которые описывают скомпенсированную нагрузку, т.е. токовые симметричные составляющие, величины фазных токов и мощностей, мгновенные значения фазных напряжений и токов и т. д.

6.   Симметризация нагрузки соединенной в звезду с нулевым проводом – исключение нулевой последовательности симметричной составляющей

В этом случае процесс компенсации состоит из двух этапов. Первый этап заключается в исключении нулевой последовательности симметричной составляющей – исключение тока в нулевом проводе. На Рис.5 выбрана схема для дальнейших рассуждений; отличающиеся минимальным значением коэффициента небаланса тока (значения элементов такие же, как в Примере 1).

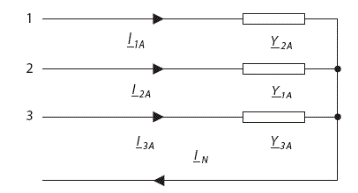
Рис.5. – Трехфазная четырехпроводная цепь – нагрузка соединена в звезду

Пример №2

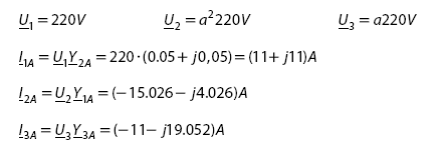
Ток в нулевом проводе:  , где  токовая симметричная составляющая нулевой последовательности.

Обратная последовательность симметричной составляющей:

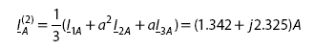
Прямая последовательность симметричной составляющей:

Коэффициент небаланса тока

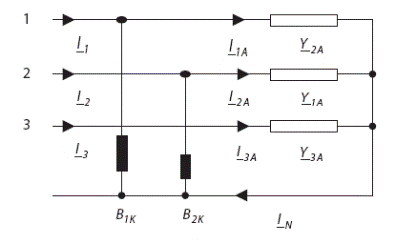
Рис.6. – Исключение составляющей нулевой последовательности (Пример 2)

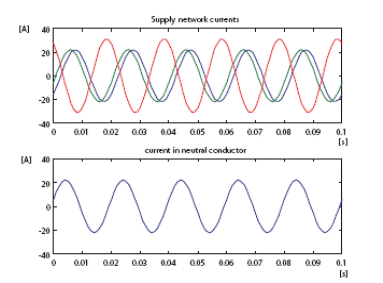
Рис.7. – Формы кривых тока: Пример 2 – перед исключением нулевой последовательности

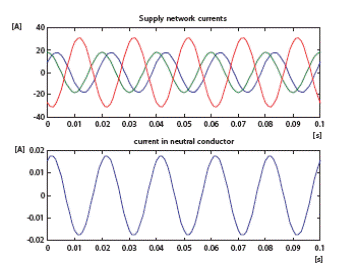
Рис.8. – Формы кривых тока: Пример 22 – после исключения нулевой последовательности

Исключение нулевой последовательности происходит с помощью двухэлементного симметризатора как на схеме-примере, показанном на Рис.6.

Питающие токи распределительной сети: