Создание модели синхронного генератора в фазных координатах. Исследование влияния демпферных обмоток на электромагнитный переходный процесс, страница 3

2.2. Модель синхронного генератора с учетом нагрузки.

Основными законами теории цепей наряду с законом Ома являются законы баланса токов в разветвлениях и баланса напряжений на замкнутых участках цепи. Таким образом, замкнутые цепи должны подчиняться законам Кирхгофа, которые говорят:

1). Алгебраическая сумма токов в узле равна нулю;

2). Алгебраическая сумма напряжений на ветвях в любом замкнутом контуре равна нулю.

Это значит, что для анализа устойчивости переходных процессов синхронного генератора требуется замкнутый контур, который представляет собой синхронный генератор – последовательное соединение нагрузки замкнутое на источник (генератор).

В общем случае последовательное соединение нагрузки представляет собой последовательность простых элементов: емкость, индуктивность и сопротивление.

Поскольку, большинство элементов электроэнергетических систем при составлении схем замещения для расчетов токов КЗ заменяются индуктивным сопротивлением, при расчёте апериодической составляющей переходят к активным сопротивлениям, то в модели потребуется учесть индуктивное сопротивление, как основную часть сопротивления элементов. Активное сопротивления также потребуется учесть, иначе длительно существующая апериодическая составляющая, затухающая только за счёт сопротивления обмоток СГ, будет присутствовать в результате работы модели. Поэтому в данной работе моделируется активно-индуктивная нагрузка и рассматривается последовательное соединение активного сопротивления и индуктивности (рис.6).

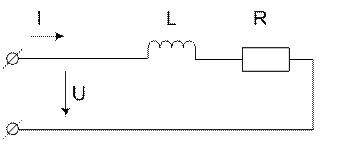
Рис. 6. R-L цепь

Исходя из вышесказанного, уравнение Кирхгофа для последовательного активно-индуктивного соединения имеет вид:

Здесь рассматривается трехфазный синхронный генератор, поэтому для придания системе замкнутого контура требуется подключить нагрузку к каждой фазе.

Получим математическую модель нагрузки, для этого выражение (6) представим в операторной форме

Из (8) следует, что 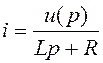. Данное выражение может быть реализовано следующим образом

Рис. 7. Модель для вычисления

Эта модель учитывает нагрузку достаточно упрощённо. Не учтены никакие нелинейности, никакие ёмкости. Таким образом, получили математическую модель нагрузки, которую, подключив к модели генератора на хх, реализуем модель синхронного генератора с учетом нагрузки.

Модель генератора в нагрузочном режиме можно представить, как и в предыдущем случае, как систему, состоящую из подсистем. При этом выходными параметрами модели будут напряжения в фазах. Входными параметрами напряжений будут токи в фазах (см. рис.9).

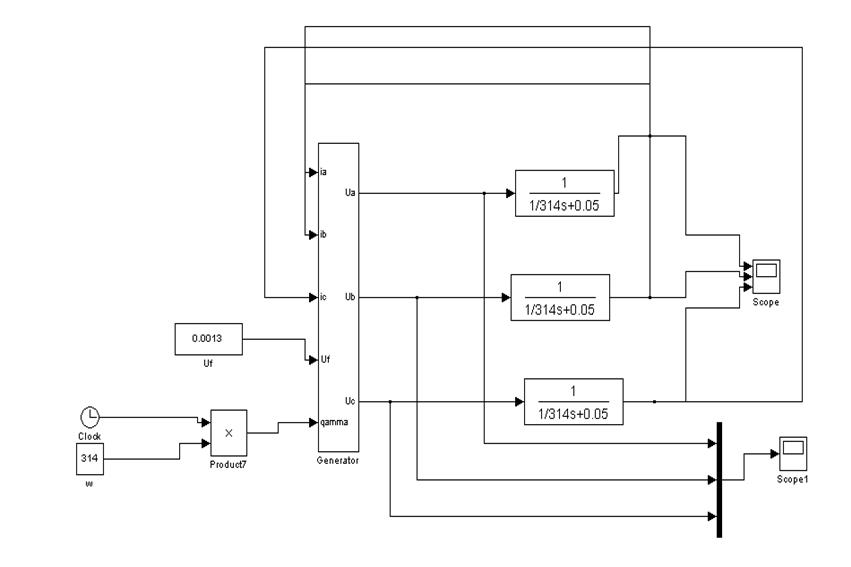
Рис. 8. Модель СГ с учетом нагрузки

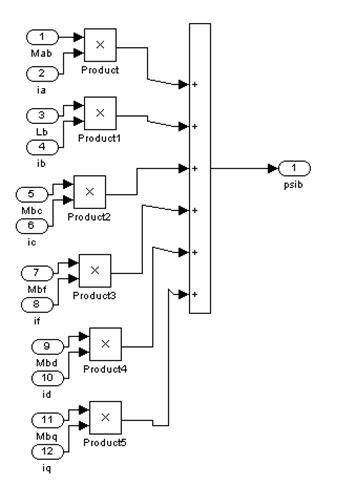
Рис. 9. Модель для вычисления  (Subsystem 2)

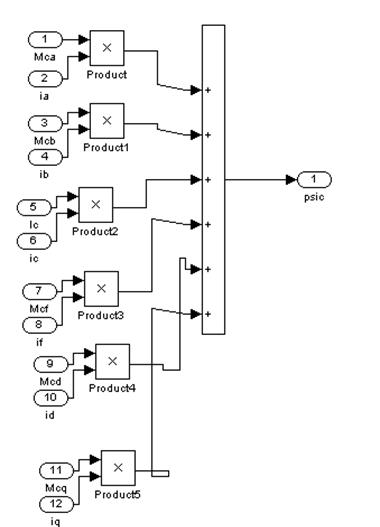
Рис. 10. Модель для вычисления  (Subsystem 4)

Рис. 11. Модель для вычисления  (Subsystem 6)

Subsystem является подсистемой для вычисления индуктивностей  и взаимоиндуктивностей

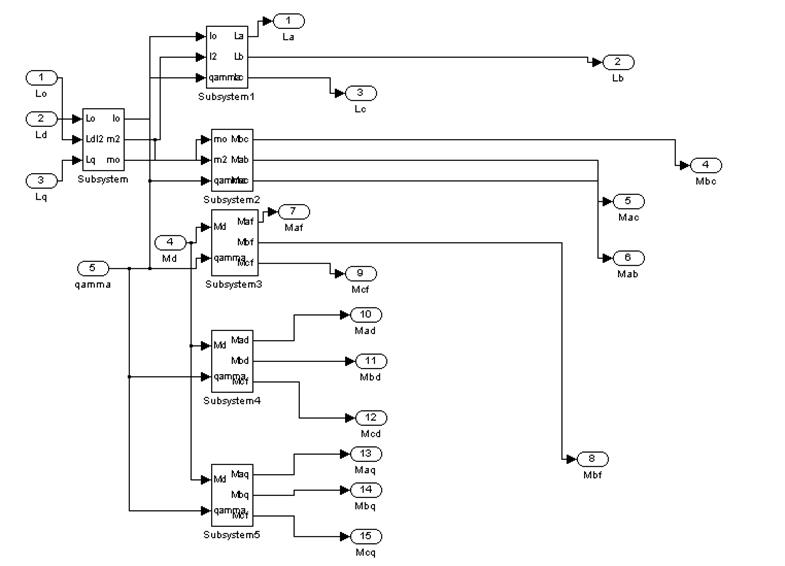
Рис. 12. Модель для вычисления  (Subsystem)

Subsystem 5, Subsystem 3, Subsystem 8 являются подсистемами для вычисления напряжений  соответственно и имеют вид:

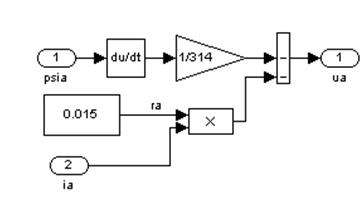
Рис. 13. Модель для вычисления  (Subsystem 5)

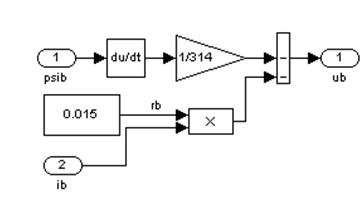
Рис. 14. Модель для вычисления  (Subsystem 3)

Рис. 15. Модель для вычисления  (Subsystem 8)

После запуска модели на рис.8 получим графики изменения фазных токов и фазных напряжений при влиянии ДО

Рис. 17. Величины фазных токов  при работе синхронного генератора с учетом нагрузки в координатах

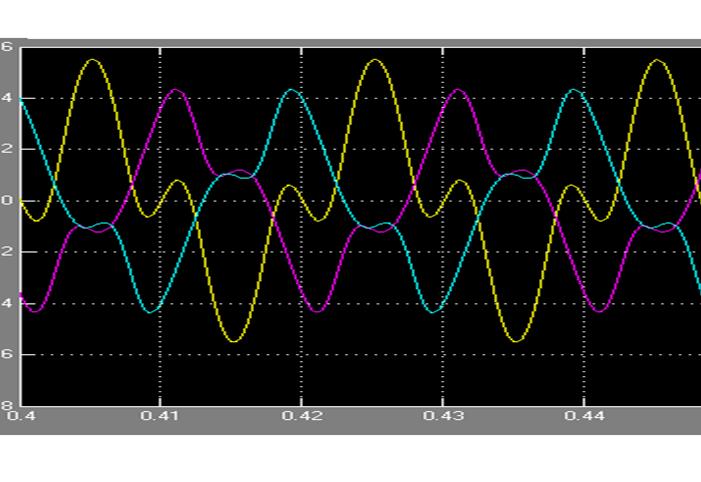
Рис. 19. Величины фазных напряжений  при работе синхронного генератора с учетом нагрузки в координатах

ЗАКЛЮЧЕНИЕ

В данной курсовой работе были рассмотрены уравнения математических моделей генератора в режиме холостого хода и с учетом нагрузки, реализация их в пакете Simulink и получение графиков изменения фазных напряжений, фазных токов и тока в обмотке возбуждения. Также была получена модель системы регулирования возбуждения пропорционального действия синхронного генератора, модель для вычисления электрической мощности и сам график ее изменения.

Использование модели синхронного генератора в фазных координатах даёт возможность более точно рассмотреть переходные процессы при различных видах повреждений. Компьютерное моделирование позволяет избежать сложных расчетов и учесть факты, относительно которых при аналитическом расчете принимались грубые допущения.

Модель СГ может быть усовершенствованна учётом влияния факторов, не рассмотренных в данной работе. Также, могут быть изменены и уточнены другие модели, использованные в работе, что позволит рассмотреть более сложные переходные процессы.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1.  Горев А.А. Переходные процессы синхронной машины. – M.: Госэнергоиздат. 1950.

2.  Методические указания к выполнению курсовой работы “Исследование на математической модели процессов в электроэнергетической системе” по курсу “Моделирование в энергетике”, Харьков НТУ “ХПИ” 2006.

3.  Конспект лекций по курсу «Моделированиев энергетике».