











4 РІВНЯННЯ ПЕРЕХІДНИХ ПРОЦЕСІВ СИНХРОННОЇ МАШИНИ У ФАЗНИХ КООРДИНАТАХ
4.1 Загальні зауваження й допущення
Аналітичне дослідження перехідних процесів машини з обліком всіх факторів, що впливають на них, представляє складне завдання. Щоб трохи спростити її, доводиться вводити ряд допущень, надаючи машині деякі властивості і якості, який вона в дійсності не володіє, тобто розглядати у відомій мірі « ідеалізовану » машину.
Розглянуті в даному розділі математичні моделі синхронного генератора (СГ) складені при наступних допущеннях:
1) Магнітна система машини ненасичена, у силу чого індуктивності машини не залежать від сил, що намагнічують (н. с).
2) Замість дійсних кривих розподілу н. с. й індукції в повітряному зазорі по розточенню статора приймають тільки їх основні, перші гармонійні, відповідно чому наведені в статорі ЕДС виражаються синусоїдами основної частоти.
3) У магнітній системі машини відсутні які-небудь втрати.
4) Конструктивне виконання машини забезпечує повну симетрію фазних обмоток статора й ротора.
При цих допущеннях найбільш точної буде модель СГ у фазних координатах А, В, С.
4.2 Вихідні рівняння
Диференціальні рівняння рівноваги ЕДС і падінь напруг у кожній з обмоток будуть:
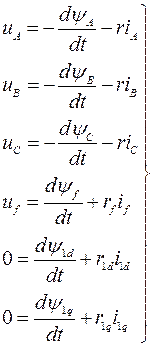 (4.1)
(4.1)
де ![]() -
активні опори відповідно для контурів кожної фази,
ланцюга порушення й демпферних обмоток;
-
активні опори відповідно для контурів кожної фази,
ланцюга порушення й демпферних обмоток;
![]() - результуючі потокосцеплення відповідних
обмоток (включаючи їх потокосцеплення розсіювання).
- результуючі потокосцеплення відповідних
обмоток (включаючи їх потокосцеплення розсіювання).
Потокосцеплення, при прийнятих допущеннях являють собою лінійні залежності від струму даного контуру й струмів магнитнозвязаних з ним інших контурів. Коефіцієнтами пропорційності при цьому будуть індуктивність L розглянутого контуру і його взаімоіндуктивности М с іншими контурами.
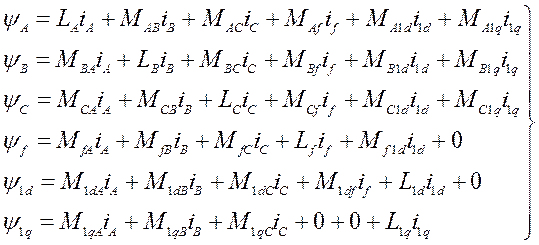 (4.2)
(4.2)
В обертовій машині тільки індуктивності ![]() можна вважати постійними. Все-таки інші L
і М залежать від положення ротора щодо обмоток статора й, отже, є
функціями часу.
можна вважати постійними. Все-таки інші L
і М залежать від положення ротора щодо обмоток статора й, отже, є
функціями часу.
Після підстановки потокосцеплень з (4.2) у систему рівнянь (4.1) одержимо систему диференціальних рівнянь зі змінними коефіцієнтами.
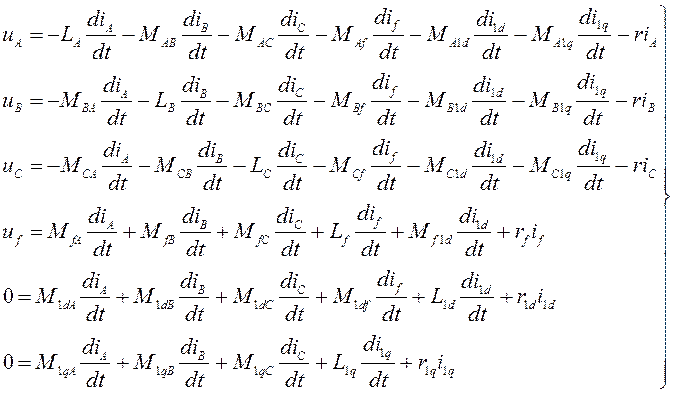 (4.3)
(4.3)
Наявність змінних коефіцієнтів, різко ускладнює рішення цієї системи. Тому до останнього часу ця математична модель СГ практично не використалася.
4.3 Індуктивності обмоток синхронної машини
Виходячи з рівнянь (4.1), (4.2), (4.3), як приклад, на рисунке 4.1 представлений верхній рівень структурної схема математичної моделі синхронного генератора у фазних координатах. З метою спрощення в цій моделі не враховуються демпферні обмотки. Як видно з рисунка структурна схема складається з 4 субсистем, кожна з яких реалізує розрахунок певних величин:
Субсистема 1 (рис. 4.2) реалізує розрахунок відповідних індуктивностей і взаімоіндуктивностей. У свою чергу субсистема 1 складається із чотирьох підсистем (1.1 - 1.4), наведено на рисунках 4.3 - 4.6.
Віртуальна модель, приведена на рисунку 4.5, реалізує рішення рівнянь
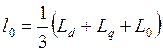 ,
,
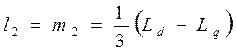 , (4.4)
, (4.4)
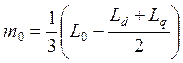 .
.
і дозволяє розрахувати постійні складові відповідних індуктивностей (l0й m0) і амплітуди других гармонік тих же індуктивностей (l2й m2).
Віртуальна модель, приведена на рисунку 4.4, реалізує рішення системи рівнянь 4.5:
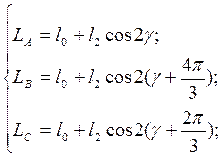 (4.5)
(4.5)
і дозволяє розрахувати індуктивності La,Lb,Lc.
Віртуальна модель, приведена на рисунке 4.5, реалізує рішення системи рівнянь 4.6:
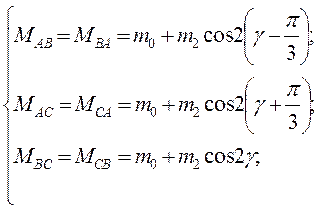 (4.6)
(4.6)
і дозволяє розрахувати взаімоіндуктивності між обмотками статора Mab, Mac, Mbc.
Віртуальна модель, приведена на рисунке 4.6, реалізує рішення системи рівнянь 4.7:
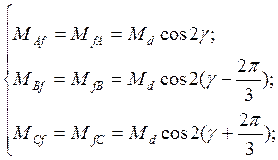 (4.7)
(4.7)
і дозволяє розрахувати взаімоіндуктивності між обмоткою збудження й обмотками статора Maf, Mbf, Mcf.
На рисунке 4.7 приведена субсистема 2 розрахунки потокосцеплення відповідних обмоток генератора, що реалізує рішення системи рівнянь 4.8:
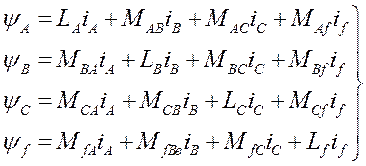 (4.8)
(4.8)
Ця субсистема складається із чотирьох підсистем 2.1-2.4. Як приклад на рисунке 4.8 приведена модель розрахунку потокосцеплення фази А в відповідності з рівнянням 1 системи 4.8 (підсистема 2.1). Підсистеми 2.2-2.4 розрахунки потокосцеплення фаз В, С й обмотки збудження по своїй структурі аналогічні підсистемі 2.1.
4.4 Математична модель СГ у фазних координатах реалізована в пакеті Matlab
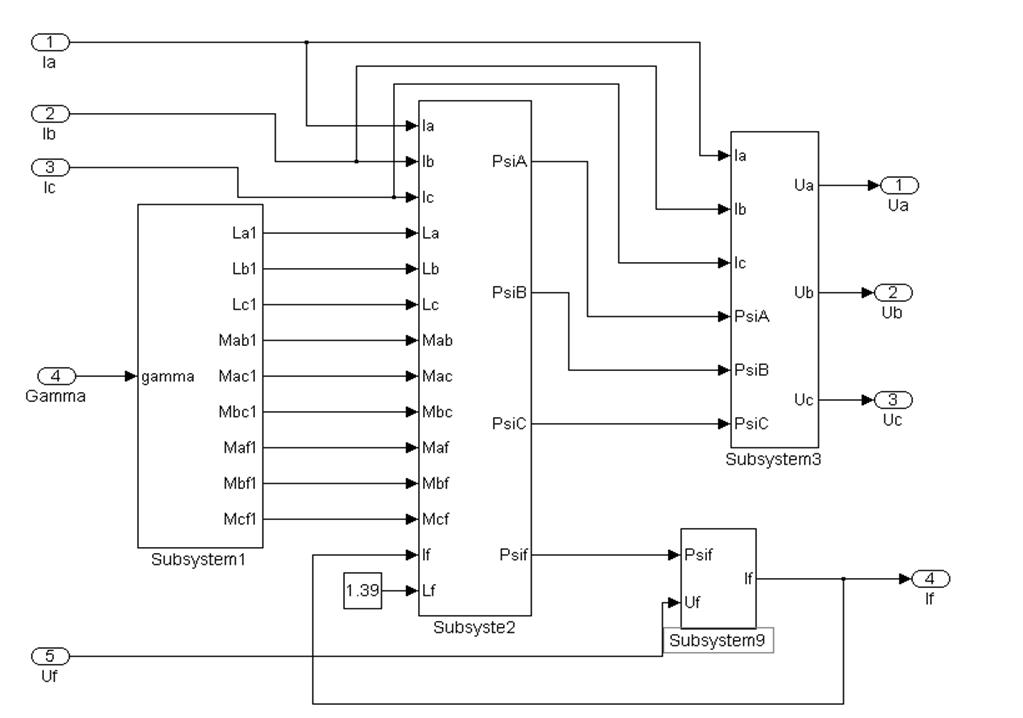
Рисунок 4.1 -Структурна схема синхронного
генератора в координатах ![]() у режимі холостого ходу
у режимі холостого ходу
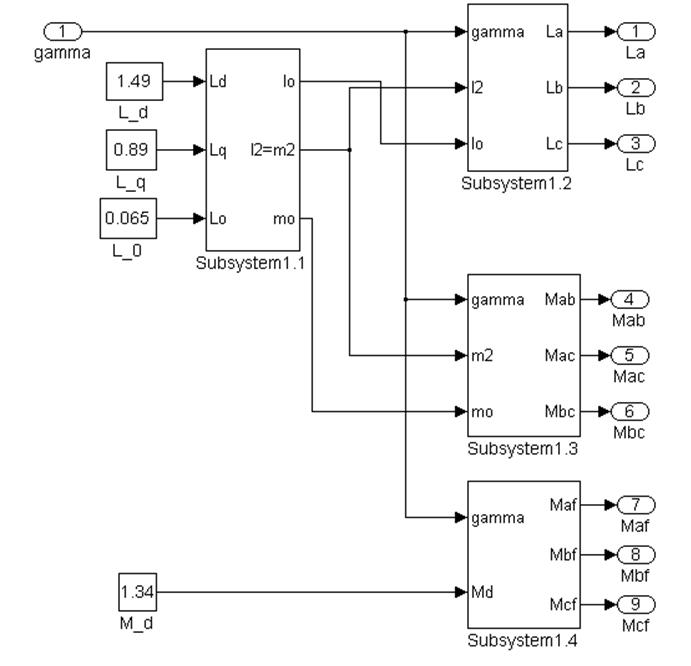
Рисунок 4.2 - Субсистема 1: структурна схема розрахунку індуктивностей і взаімоіндуктивностей
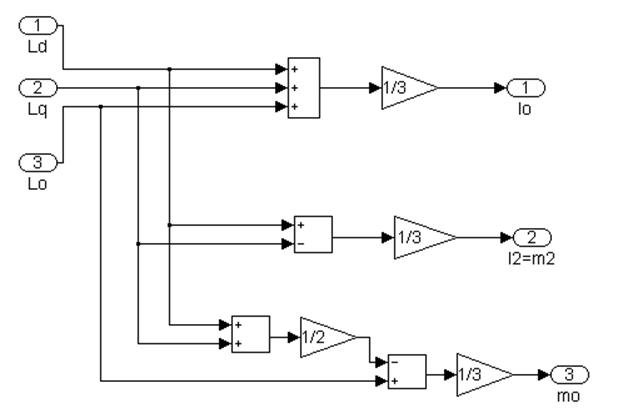
Рисунок 4.3 -Підсистема 1.1. Розрахунок коефіцієнтів
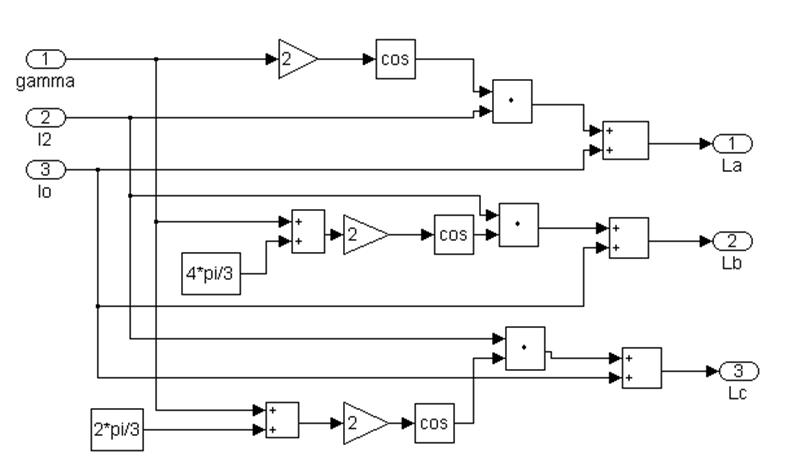
Рисунок 4.4 -Підсистема 1.2. Розрахунок індуктивностей La,Lb,Lc
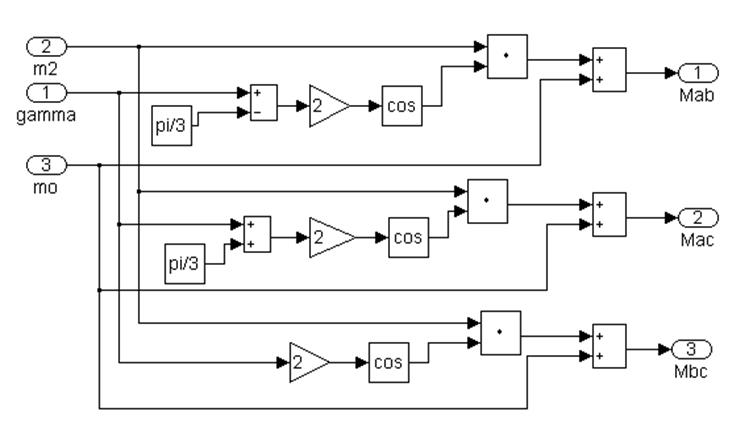
Рисунок 4.5 -Підсистема 1.3. Розрахунок взаімоіндуктивностей між обмотками статора Mab, Mac, Mbc
Ця модель і багато наступні буде підсистемою іншої моделі, для зовнішньої моделі будуть доступні тільки входи (In) і виходи (Out).
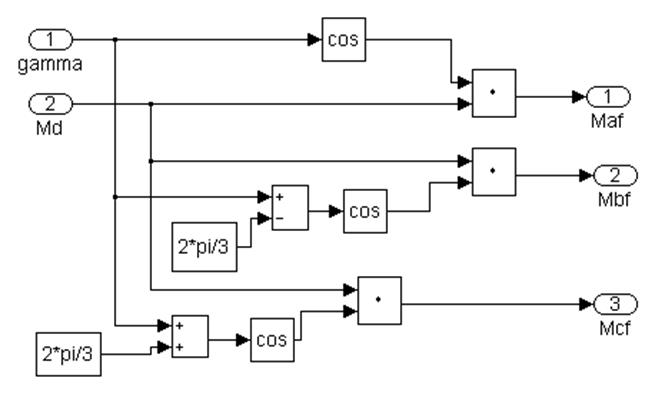
Рисунок 4.6 -Підсистема 1.4. Розрахунок взаімоіндуктивностей між обмоткою збудження й обмотками статора Maf, Mbf, Mcf.
На рисунке 4.9,субсистема 3 реалізує рішення системи рівнянь 4.9 і дозволяє змоделювати фазні напруги генератора.
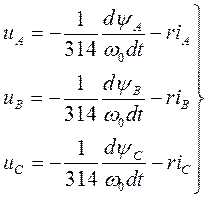 (4.9)
(4.9)
Субсистема 4, представлена на рисунке 4.10, моделює струм в обмотці збудження відповідно до рівняння:
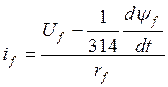 (4.10)
(4.10)
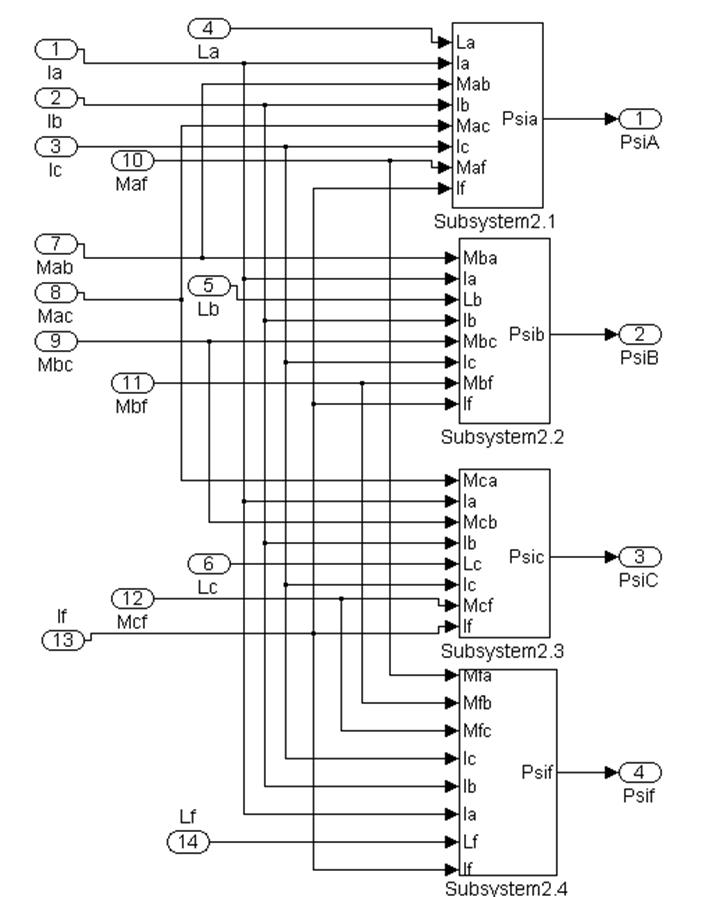
Рисунок 4.7 -Субсистема 2 Структурна схема розрахунку потокосцеплення
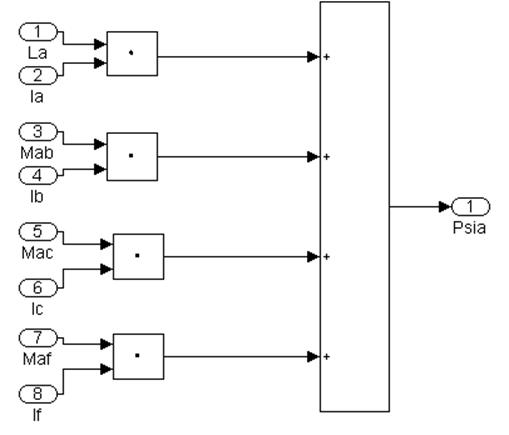
Рисунок 4.8. - Підсистема 2.1. Розрахунок потокосцеплення фази А.
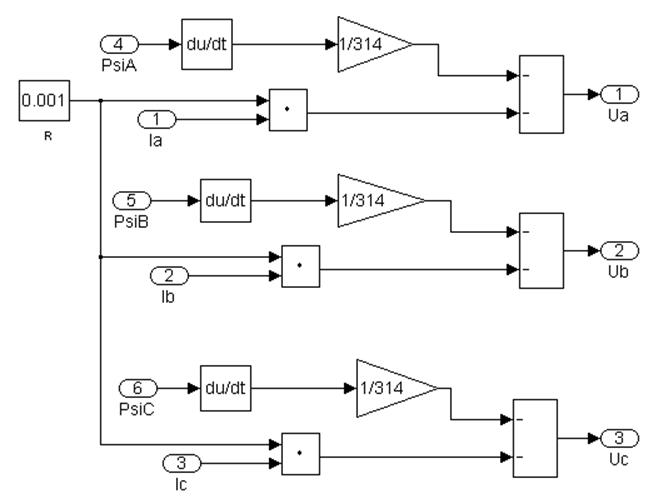
Рисунок 4.9 -Субсистема 3. Розрахунок фазних напруг генератора.
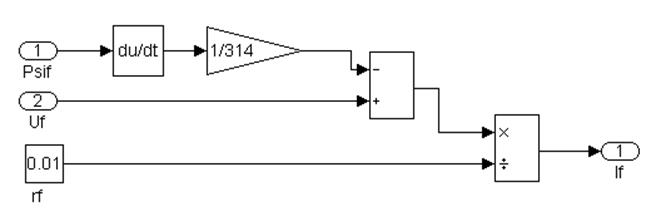
Рисунок 4.10 - Субсистема 4. Розрахунок струму в обмотці збудження
Модель генератора можна скласти як підсистему, що складається з описаних вище підсистем.
При цьому вихідними параметрами моделі будуть напруги у фазах. Вхідними параметрами напруг будуть струми у фазах. Залежність струмів від напруг буде визначатися режимом роботи енергосистемою, модель режиму роботи буде розташовуватися поза моделлю генератора.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.