исследовании электромагнитных переходных процессов не учитывают изменение вращения скорости генератора.
2 Математическая модель синхронного генератора в фазных координатах
Наиболее точно можно описать процессы, протекающие в СГ, используя математическую модель генератора в фазных координатах.
При составлении этой модели, в целях упрощения, не будем учитывать демпферные обмотки. Следовательно, уравнение баланса напряжений имеет вид:
Уравнение статора: Уравнение ротора:
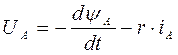
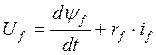
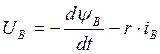 (1)
(1)
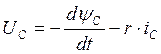
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() - мгновенные значения напряжений обмоток статора и
ротора;
- мгновенные значения напряжений обмоток статора и
ротора;
![]() ,
, ![]() ,
, ![]() ,
, ![]() - потокосцепления, связанные с соответствующими
обмотками;
- потокосцепления, связанные с соответствующими
обмотками;
![]() ,
, ![]() ,
, ![]() ,
, ![]() - мгновенные токи, протекающие в свободных
обмотках.
- мгновенные токи, протекающие в свободных
обмотках.
![]()
![]() (2)
(2)
![]()
![]()
где ![]() и
и ![]() - индуктивности и взаимоиндуктивности
соответствующих обмоток.
- индуктивности и взаимоиндуктивности
соответствующих обмоток.
Система уравнений 1 после подставления в неё значений из уравнений 2 превращается в систему из 4 дифференциальных уравнений с переменными коэффициентами, т.к. практически все индуктивности и взаимоиндуктивности – переменные величины, т.е. являются функцией времени (вращение ротора генератора) за исключением индуктивной обмотки возбуждения.
![]() const
const
Т.к. за один оборот ротора магнитное поле меняет своё значение дважды, то эти переменные коэффициенты меняются периодически с двойной частотой и их можно расчитать по формулам:
![]() cos
cos![]()
![]() cos
cos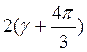
![]() cos
cos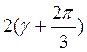 (3)
(3)
![]() cos
cos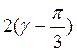
![]() cos
cos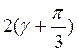
![]() cos
cos![]() (4)
(4)
![]() cos
cos![]()
![]() cos
cos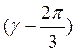
![]() cos
cos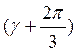 (5)
(5)
Эти коэффициенты оказываются непостоянными из-за электрической и магнитной несимметрии ротора генератора. Т. о. система уравнений 1 и 2 позволяет смоделировать процессы в СГ в фазных координатах в режиме ХХ.
Чтобы смоделировать СГ в нагруженном режиме или в режиме КЗ необходимо добавить систему уравнений, позволяющую найти токи в обмотках статора и ротора.
3 Реализация модели синхронного генератора в фазных координатах
С целью упрощения модели представим её в виде 9 суперблоков. Первый суперблок моделирует переменные коэффициенты в уравнения для определения потокосцепления. Суперблоки 2,3,4,5 моделируют потокосцепление, 6,7,8 - фазное напряжение, 9-й – ток в обмотках возбуждения.
Первый
суперблок в свою очередь состоит из подблоков. Первые три моделируют постоянные
коэффициенты ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; подблоки 4 – 6 моделируют индуктивности
; подблоки 4 – 6 моделируют индуктивности ![]() ,
, ![]() ,
, ![]() ; подблоки 7 – 9 моделируют взаимоиндукцию между
фазами
; подблоки 7 – 9 моделируют взаимоиндукцию между
фазами ![]() ,
, ![]() ,
, ![]() ; подблоки 10 – 12 моделируют взаимоиндукцию между
обмотками возбуждения и фазными обмотками статора.
; подблоки 10 – 12 моделируют взаимоиндукцию между
обмотками возбуждения и фазными обмотками статора.
Порядок выполнения работы
I. Реализация первого суперблока
1. При
реализации модели СГ в первую очередь необходимо смоделировать постоянные
коэффициенты ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Первый подблок имеет следующую реализацию:
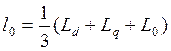
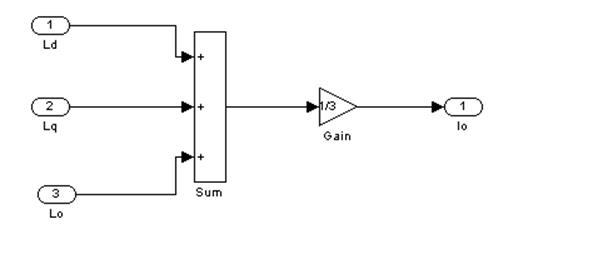
Рис.1
– Первый подблок первого суперблока, моделирующий ![]()
Реализация второго подблока:
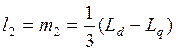
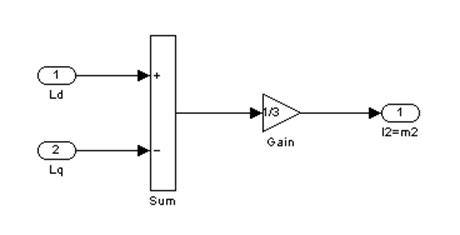
Рис.2
– Второй подблок первого суперблока, моделирующий ![]() ,
, ![]()
Реализация третьего подблока:
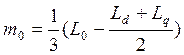
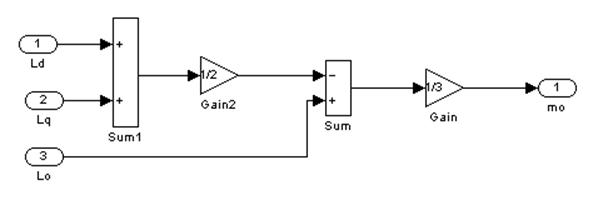
Рис.3
– Третий подблок первого суперблока, моделирующий ![]()
Каждый из трёх подблоков представляем в виде субблоков. Для этого:
а) выделяем подблок;
б) с помощью правой кнопки мыши находим операцию “Create subsystem”;
в) образуем субблок;
г) обозначаем входящие и выходящие параметры.
2.
Моделирование индуктивностей ![]() ,
, ![]() ,
, ![]() согласно системе уравнений 3 с помощью трёх подблоков.
В этой системе уравнений
согласно системе уравнений 3 с помощью трёх подблоков.
В этой системе уравнений
![]() =
= ![]() ;
;
![]() - переход времени от секунд к
о.е.
- переход времени от секунд к
о.е.
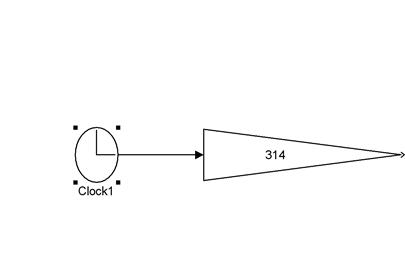
Рис. 4
– Модель ![]()
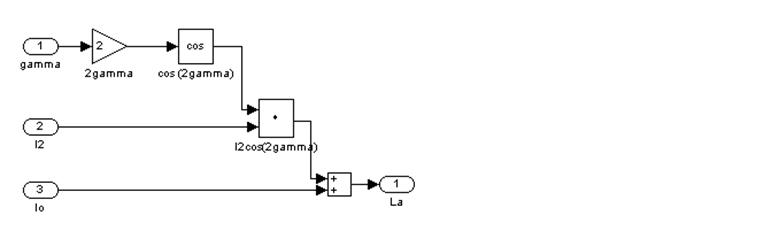
Рис. 5 – Четвертый подблок первого суперблока, моделирующий LA
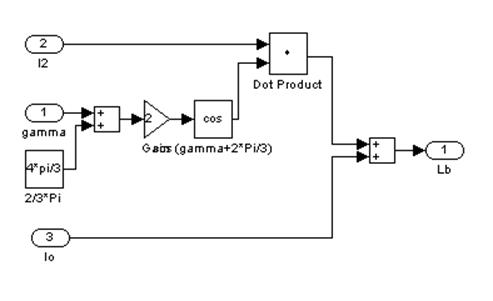
Рис. 6 – Пятый подблок первого суперблока, моделирующий LВ
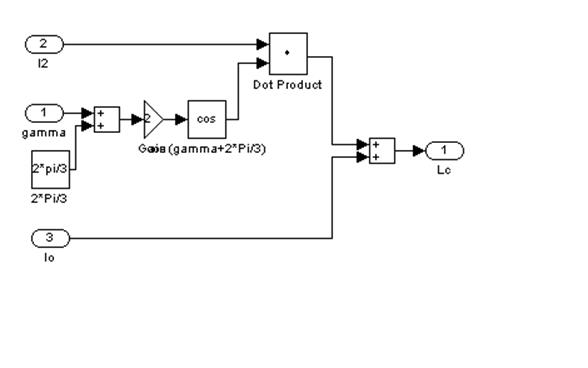
Рис. 7 – Шестой подблок первого суперблока, моделирующий LС
3. Моделирование
взаимоиндуктивностей между фазами ![]() ,
, ![]()
Согласно системе уравнений (4):
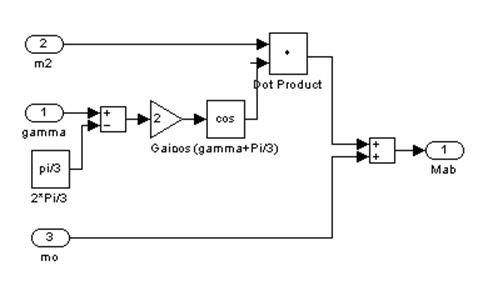
Рис. 8 – Седьмой подблок первого суперблока, моделирующий МАВ,
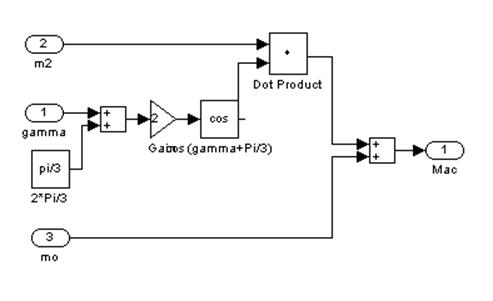
Рис. 9 – Восьмой подблок первого суперблока, моделирующий МАС
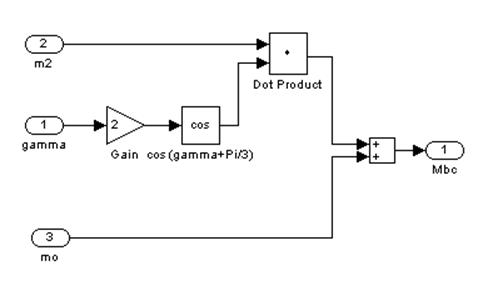
Рис. 10 – Девятый подблок первого суперблока, моделирующий МВС
4. Моделирование
взаимоиндуктивностей между обмоткой возбуждения и фазными обмотками ![]()
![]() ,
, ![]() проводится согласно системе уравнений
(5):
проводится согласно системе уравнений
(5):
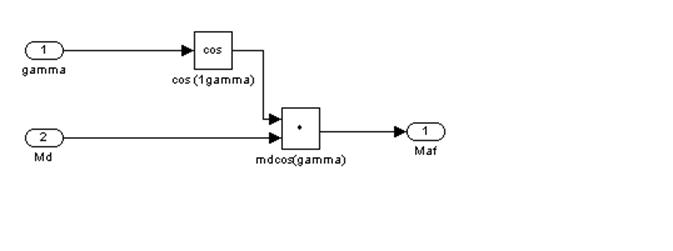
Рис. 11 – Десятый подблок первого суперблока, моделирующий МAF
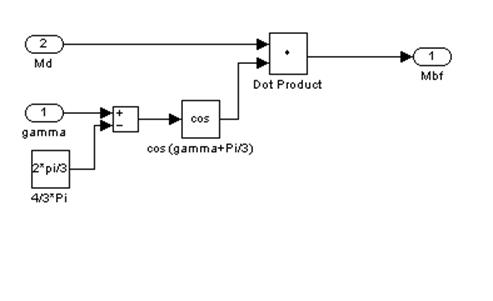
Рис. 12 – Одиннадцатый подблок первого суперблока, моделирующий МВF
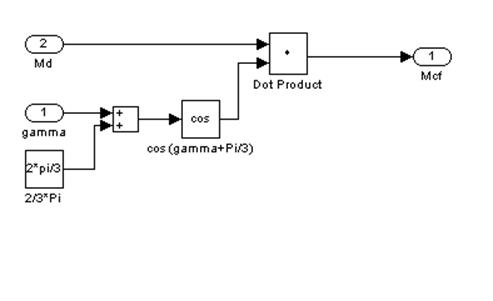
Рис. 13 – Двенадцатый подблок первого суперблока, моделирующий МСF
4 Первый субблок будет иметь вид:
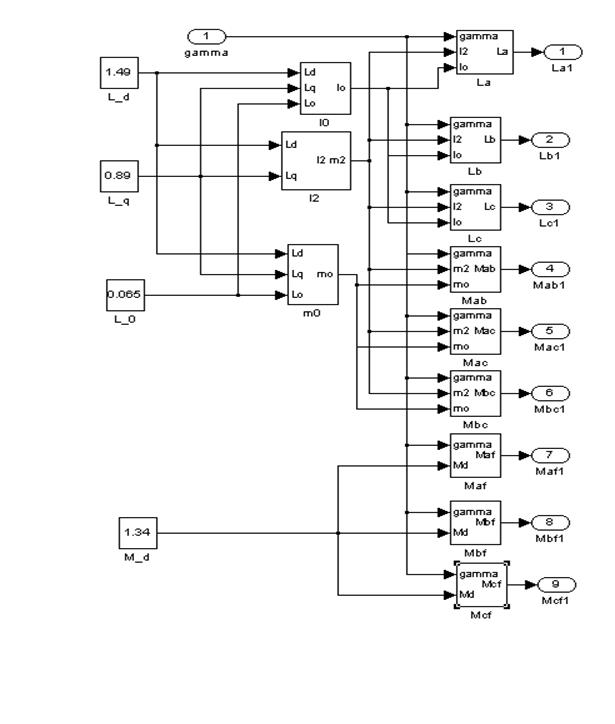
Рис. 14 – Содержимое первого суперблока
5. Образуем первый суперблок.
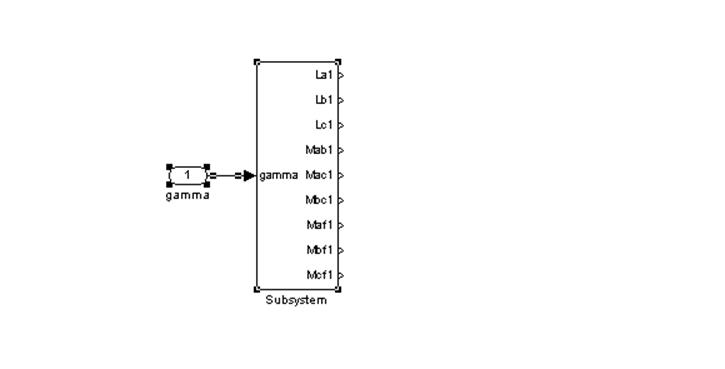
Рис. 15 – Первый суперблок
II. Реализация 2 суперблока
Согласно системе уравнений (2) моделируем потокосцепления, связанные с соответствующими обмотками.
![]()
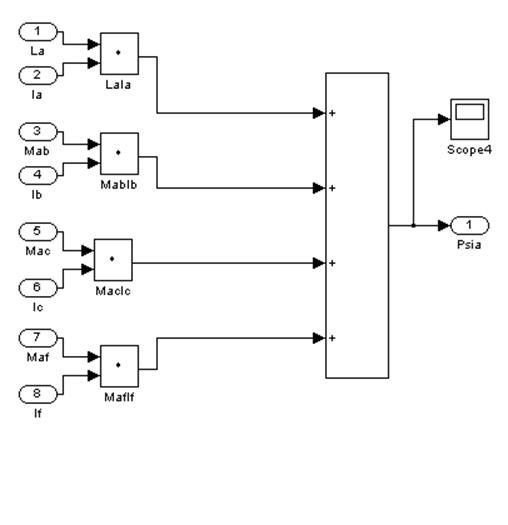
Рис. 16 – Первый подблок второго суперблока
![]()
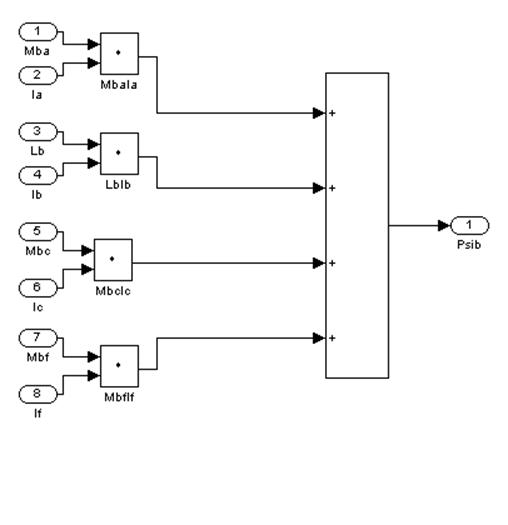
Рис. 17 – Второй подблок второго суперблока
![]()
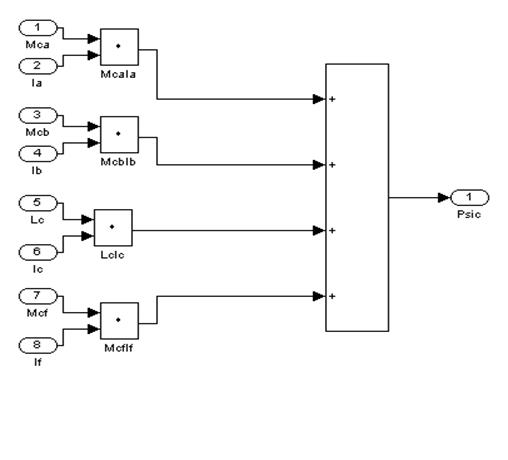
Рис. 18 – Третий подблок второго суперблока
![]()
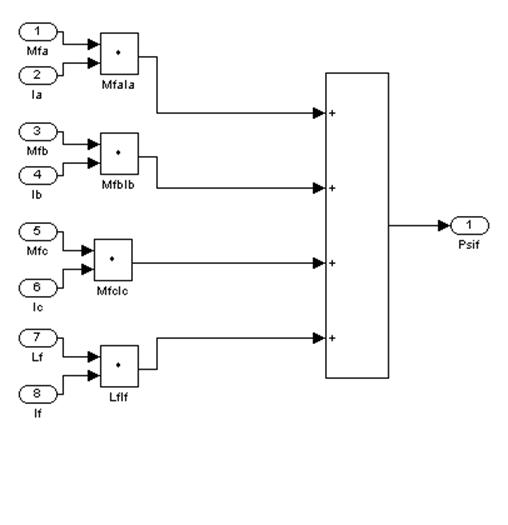
Рис. 19 – Четвёртый подблок второго суперблока
Согласно системе уравнений (1) находим напряжение в обмотке статора. Для этого также составляем 3 подблока во втором суперблоке.
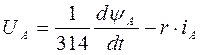
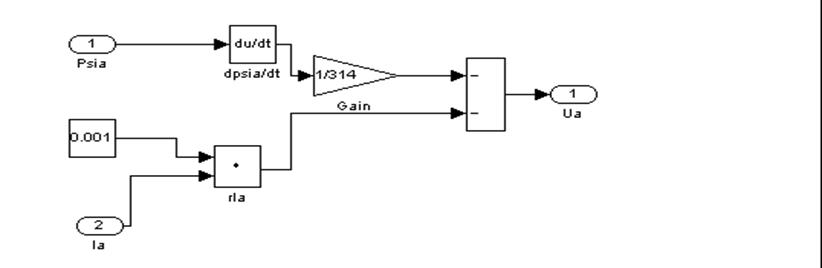
Рис. 20 – Пятый подблок второго суперблока
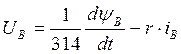
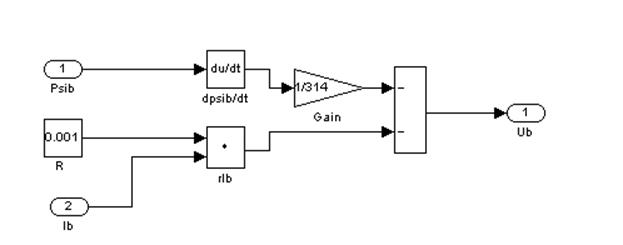
Рис. 21 – Шестой подблок второго суперблока
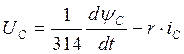
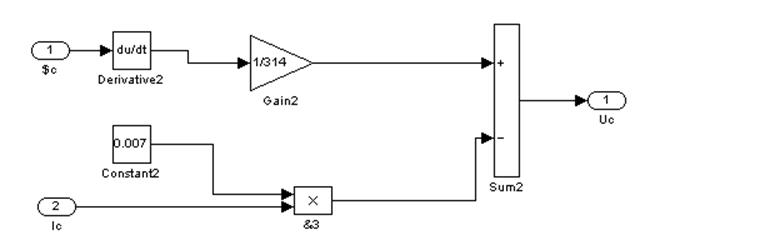
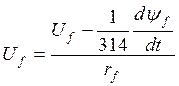
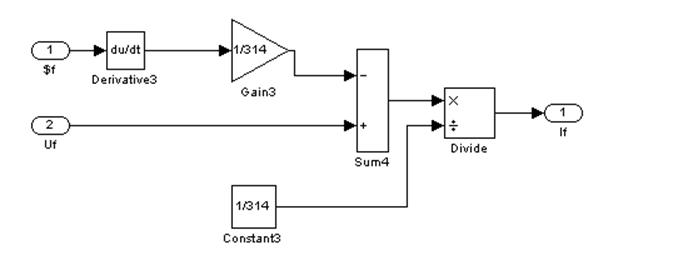
Рис. 23 – Восьмой подблок второго суперблока
В итоге получаем второй суперблок.
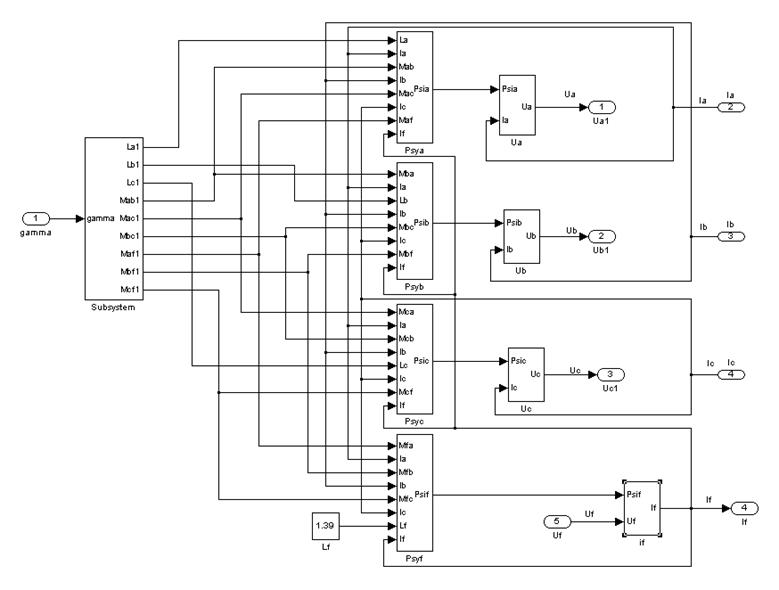
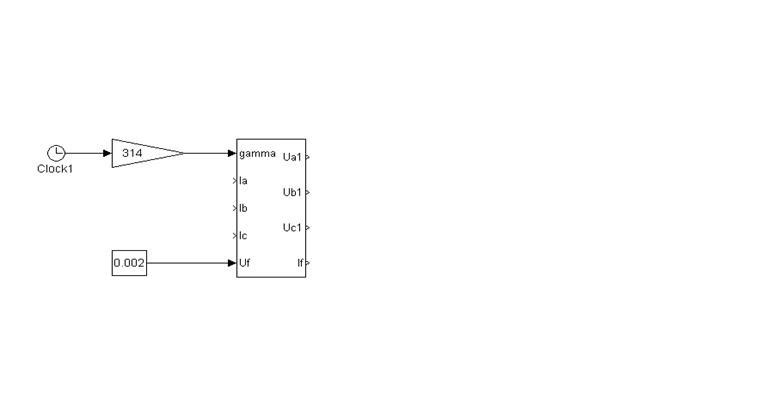
Рис. 25 – Второй суперблок
4 Модель СГ в режиме ХХ
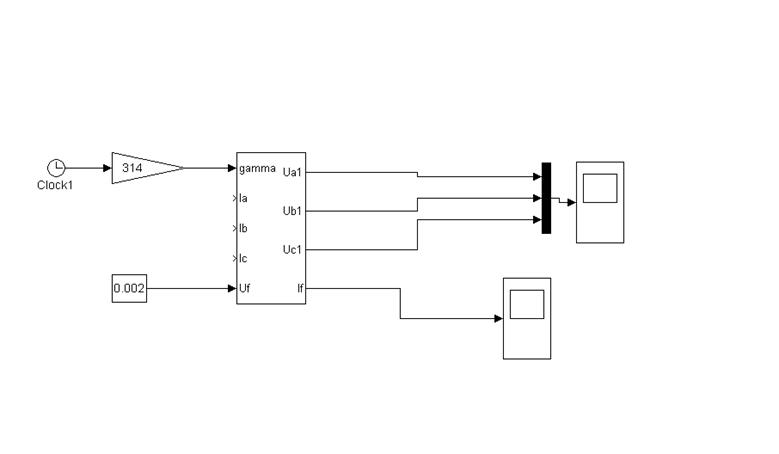
Подключив осциллографы к
соответствующим выходам второго суперблока, будем наблюдать изменение фазных
напряжений и тока в обмотке возбуждения СГ в режиме ХХ. С помощью  объединяем фазные напряжения
для просмотра в одной системе координат. Т.к. в данной модели фазные токи равны
0, то это модель СГ в режиме ХХ.
объединяем фазные напряжения
для просмотра в одной системе координат. Т.к. в данной модели фазные токи равны
0, то это модель СГ в режиме ХХ.
5 МОДЕЛЬ СГ ПОД НАГРУЗКОЙ
Нагрузку СГ можно
выразить через 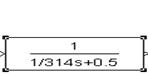 . Добавим
этот элемент в каждую фазу. Затем подадим токи. В итоге СГ под нагрузкой будет
иметь вид:
. Добавим
этот элемент в каждую фазу. Затем подадим токи. В итоге СГ под нагрузкой будет
иметь вид:
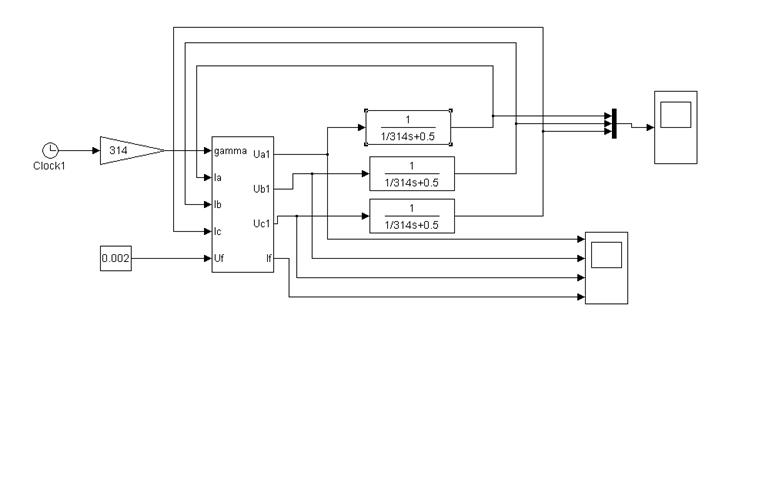
6 МЕЖВИТКОВОЕ ЗАМЫКАНИЕ ОБМОТКИ СТАТОРА СГ
При межвитковом замыкании в одной из обмоток статора (например, А) появляется новый контур, который является короткозамкнутым и также влияет на все остальный обмотки. Также уменьшается количество витков в той обмотке, где произошло межвитковое замыкание, на число витков равное числу витков в короткозамкнутом контуре.
Т.к все расчёты проводятся в относительных единицах, то при нормальном режиме работы СГ количество витков не учитывается, т.к оно равно 1. При межвитковом замыкании мы будем учитывать количество витков в процентном соотношении.
При межвитковом замыкании системы уравнений (1)-(5) будут иметь следующий вид:
Уравнение статора: Уравнение ротора:
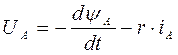
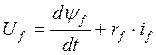
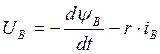 (6)
(6)
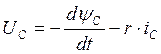
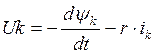 , где
, где ![]() - напряжение в
короткозамкнутом контуре;
- напряжение в
короткозамкнутом контуре;
![]() - потокосцепление короткозамкнутого контура;
- потокосцепление короткозамкнутого контура;
![]() - мгновенный ток в той же обмотке.
- мгновенный ток в той же обмотке.
![]()
![]() (7)
(7)
![]()
![]()
![]()
где ![]() и
и ![]() - индуктивности и взаимоиндуктивности
соответствующих обмоток.
- индуктивности и взаимоиндуктивности
соответствующих обмоток.
![]() cos
cos![]()
![]() cos
cos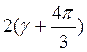
![]() cos
cos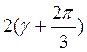 (8)
(8)
![]() cos
cos![]() ,
,
![]() cos
cos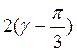
![]() cos
cos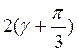
![]() cos
cos![]() (9)
(9)
![]() cos
cos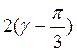
![]() cos
cos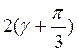
![]() cos
cos![]() ,
,
![]() cos
cos![]()
![]() cos
cos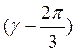
![]() cos
cos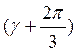 (10)
(10)
![]() cos
cos![]()
Также допустим, что замкнулась 10% втков в обмотке А.
Согласно этим системам уравнений математическая модель СГ будет
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.